题目内容
20.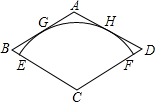 在菱形ABCD中,∠A=120°,AB=2$\sqrt{3}$,以点C为圆心的弧$\widehat{EF}$,分别与AB、AD相切于G、H,与BC、CD分别相交于点E、F,用扇形CEF做成圆锥的侧面,则圆锥的底面圆的半径为( )
在菱形ABCD中,∠A=120°,AB=2$\sqrt{3}$,以点C为圆心的弧$\widehat{EF}$,分别与AB、AD相切于G、H,与BC、CD分别相交于点E、F,用扇形CEF做成圆锥的侧面,则圆锥的底面圆的半径为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | 1 |
分析 先连接CG,设CG=R,由勾股定理求得R,根据弧长公式l=$\frac{nπR}{180}$,再由2π•r=$\frac{nπR}{180}$,求出r即可.
解答 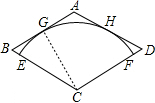 解:如图:连接CG,
解:如图:连接CG,
∵∠A=120°,
∴∠B=60°,
∵AB与$\widehat{EF}$相切,
∴CG⊥AB,
在直角△CBG中,∠B=60°,BC=AB=2$\sqrt{3}$,
∴CG=3,即:R=3.
设圆锥底面的半径为r,则:2πr=$\frac{nπr}{180}$=$\frac{120π×3}{180}$.
∴r=1.
故选D.
点评 本题考查的是圆锥的计算,先利用直角三角形求出扇形的半径,运用弧长公式计算出弧长,然后根据底面圆的周长等于扇形的弧长求出底面圆的半径.

练习册系列答案
相关题目
9.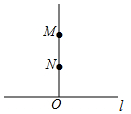 如图,已知ON⊥l,OM⊥l,所以OM与ON重合,这个推理的根据是( )
如图,已知ON⊥l,OM⊥l,所以OM与ON重合,这个推理的根据是( )
 如图,已知ON⊥l,OM⊥l,所以OM与ON重合,这个推理的根据是( )
如图,已知ON⊥l,OM⊥l,所以OM与ON重合,这个推理的根据是( )| A. | 过一点只能作一条垂线 | |
| B. | 过两点只能作一条垂线 | |
| C. | 垂线段最短 | |
| D. | 经过一点有且只有一条直线垂直于已知直线 |
 如图,点C是线段AB上的点,点D是线段BC的中点,若AB=10cm,AC=6cm,求AD的长.
如图,点C是线段AB上的点,点D是线段BC的中点,若AB=10cm,AC=6cm,求AD的长. 已知:如图,在△ABC中,∠C=90°
已知:如图,在△ABC中,∠C=90° 如图,线段AD,BC相交于点O,已知OA=4,OB=3,OC=9,OD=12,C,D,E三点在一直线上,求证:∠A+∠EDO=180°.
如图,线段AD,BC相交于点O,已知OA=4,OB=3,OC=9,OD=12,C,D,E三点在一直线上,求证:∠A+∠EDO=180°.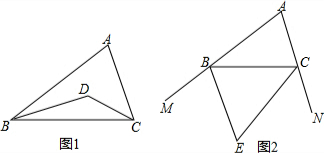 (1)如图1,在△ABC中,BD、CD分别是△ABC两个内角∠ABC、∠ACB的平分线.
(1)如图1,在△ABC中,BD、CD分别是△ABC两个内角∠ABC、∠ACB的平分线. 图中的几何体是由三个大小相同的正方体组成的,它的主视图为( )
图中的几何体是由三个大小相同的正方体组成的,它的主视图为( )



 已知:如图,AE2=AD•AB,且∠ABE=∠ACB.试说明:DE∥BC.
已知:如图,AE2=AD•AB,且∠ABE=∠ACB.试说明:DE∥BC.