题目内容
20.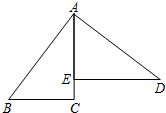 如图,AB=AD,∠BAD=90°,AC⊥BC于点C,DE⊥AC于点E,且AB=5,BC=3,则CE=1.
如图,AB=AD,∠BAD=90°,AC⊥BC于点C,DE⊥AC于点E,且AB=5,BC=3,则CE=1.
分析 利用垂直得到∠ACB=∠AED=90°,则∠B+∠BAC=90°,再根据等角的余角相等得到∠B=∠DAE,然后根据全等三角形的判定方法得到△ABC≌△DAE,于是BC=AE=3,再根据勾股定理可计算出AC=3,最后利用CE=AC-AE进行计算即可.
解答 解:∵AC⊥BC,DE⊥AC,
∴∠ACB=∠AED=90°,
∴∠B+∠BAC=90°,
∵∠BAD=90°,
∴∠BAC+∠DAE=90°,
∴∠B=∠DAE,
在△ABC和△DAE中
$\left\{\begin{array}{l}{AB=AD}\\{∠B=∠EAD}\\{∠ACB=∠DEA}\end{array}\right.$,
∴△ABC≌△DAE,
∴BC=AE,
而BC=3,
∴AE=3,
在Rt△ABC中,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=4,
∴CE=AC-AE=4-3=1.
故答案为1.
点评 本题考查了全等三角形的判定与性质:有两组角分别相等,且其中一组角所对的边对应相等,那么这两个三角形全等;全等三角形的对应边相等.也考查了勾股定理.

练习册系列答案
相关题目
15.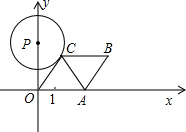 如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B.C点都在第一象限内,且AO=AC,又以P(0,4$\sqrt{3}$)为圆心,PC为半径的圆恰好与OC所在的直线相切,则t=( )
如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B.C点都在第一象限内,且AO=AC,又以P(0,4$\sqrt{3}$)为圆心,PC为半径的圆恰好与OC所在的直线相切,则t=( )
 如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B.C点都在第一象限内,且AO=AC,又以P(0,4$\sqrt{3}$)为圆心,PC为半径的圆恰好与OC所在的直线相切,则t=( )
如图所示,已知A点从(1,0)点出发,以每秒1个单位长的速度沿着x轴的正方向运动,经过t秒后,以O、A为顶点作菱形OABC,使B.C点都在第一象限内,且AO=AC,又以P(0,4$\sqrt{3}$)为圆心,PC为半径的圆恰好与OC所在的直线相切,则t=( )| A. | 2$\sqrt{3}$-1 | B. | 2$\sqrt{3}$+1 | C. | 5 | D. | 7 |
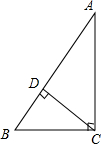 在△ABC中,∠ACB=90°,BC=3,AC=4,CD⊥AB,D为垂足.求BD的长.
在△ABC中,∠ACB=90°,BC=3,AC=4,CD⊥AB,D为垂足.求BD的长. 如图,黑板上的题目小明不会做,请你帮他填上x=0或x=7.
如图,黑板上的题目小明不会做,请你帮他填上x=0或x=7.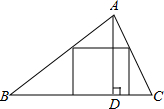 如图,△ABC是一块锐角三角形材料,边BC=80mm,高AD=60mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是$\frac{240}{7}$mm.
如图,△ABC是一块锐角三角形材料,边BC=80mm,高AD=60mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是$\frac{240}{7}$mm.