题目内容
10.求适合下列条件的锐角α:(1)cosα=$\frac{1}{2}$;
(2)tanα=$\frac{\sqrt{3}}{3}$;
(3)sin2α=$\frac{\sqrt{2}}{2}$;
(4)2sinα-$\sqrt{2}$=0.
分析 (1)、(2)、(3)直接根据锐角三角函数的定义即可得出结论;(4)先求出sinα的值,再由锐角三角函数的定义即可得出结论.
解答 解:(1)∵cosα=$\frac{1}{2}$,α为锐角
∴α=60°;
(2)∵tanα=$\frac{\sqrt{3}}{3}$,α为锐角,
∴α=30°;
(3)∵sin2α=$\frac{\sqrt{2}}{2}$,
∴2α=45°,
∴α=22.5°;
(4)∵2sinα-$\sqrt{2}$=0,
∴sinα=$\frac{\sqrt{2}}{2}$,
∵α为锐角,
∴α=45°.
点评 本题考查的是特殊角的三角函数值,熟记各特殊角的三角函数值是解答此题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
15.如图,在数轴上表示互为相反数的两数的点是( )


| A. | 点A和点C | B. | 点B和点A | C. | 点C和点B | D. | 点D和点B |
2.在数轴上a所对应的点与b所对应的点相差6个单位长度,若-a=2,则b等于( )
| A. | 4 | B. | -4 | C. | -8 | D. | 4或-8 |
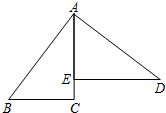 如图,AB=AD,∠BAD=90°,AC⊥BC于点C,DE⊥AC于点E,且AB=5,BC=3,则CE=1.
如图,AB=AD,∠BAD=90°,AC⊥BC于点C,DE⊥AC于点E,且AB=5,BC=3,则CE=1.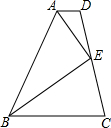 已知:如图,AD∥BC,点E是DC的中点,BE平分∠ABC,求证:AE平分∠BAD.
已知:如图,AD∥BC,点E是DC的中点,BE平分∠ABC,求证:AE平分∠BAD. 如图是一名考古学家发现的一块古代车轮的碎片,你能帮他找出这个轮子的半径吗?说出你的理由.
如图是一名考古学家发现的一块古代车轮的碎片,你能帮他找出这个轮子的半径吗?说出你的理由.