题目内容
10.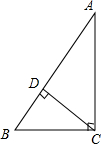 在△ABC中,∠ACB=90°,BC=3,AC=4,CD⊥AB,D为垂足.求BD的长.
在△ABC中,∠ACB=90°,BC=3,AC=4,CD⊥AB,D为垂足.求BD的长.
分析 在直角三角形ABC中,利用勾股定理求出AB的长,再利用面积法求出CD的长,然后由勾股定理求出BD的长即可.
解答 解:在△ABC中,∠ACB=90°,CD⊥AB,BC=3,AC=4,
由勾股定理得:AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
∵S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,
∴CD=$\frac{AC•BC}{AB}$=$\frac{4×3}{5}$=2.4,
∴BD=$\sqrt{{BC}^{2}-C{D}^{2}}$=$\sqrt{{3}^{2}-2.{4}^{2}}$=1.8.
点评 此题考查了勾股定理以及三角形面积求法,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,E,F分别是矩形ABCD一组对边AD,CB的中点,已知矩形AEFB∽矩形ABCD,求AB:BC的值.
如图,E,F分别是矩形ABCD一组对边AD,CB的中点,已知矩形AEFB∽矩形ABCD,求AB:BC的值.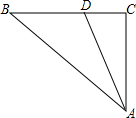 Rt△ABC中,∠C=90°,AC=3,BC=4,动点D在边BC上从点C向点B运动,连接AD,点C关于直线AD的对称点为点P,若△BCP为等腰三角形,则CP2的值为16或18-6$\sqrt{5}$或$\frac{576}{25}$.
Rt△ABC中,∠C=90°,AC=3,BC=4,动点D在边BC上从点C向点B运动,连接AD,点C关于直线AD的对称点为点P,若△BCP为等腰三角形,则CP2的值为16或18-6$\sqrt{5}$或$\frac{576}{25}$. 如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,DE=2cm,AB=8cm.求:⊙O的半径.
如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,DE=2cm,AB=8cm.求:⊙O的半径.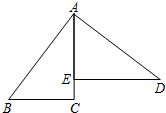 如图,AB=AD,∠BAD=90°,AC⊥BC于点C,DE⊥AC于点E,且AB=5,BC=3,则CE=1.
如图,AB=AD,∠BAD=90°,AC⊥BC于点C,DE⊥AC于点E,且AB=5,BC=3,则CE=1.