题目内容
1.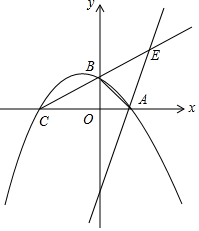 如图,二次函数y=-$\frac{1}{2}$(x+2)(x-1)图象与坐标轴的交点分别为A,B,C三点,点E是射线CB上第一象限内一点,记点C、B到直线AE的距离分别为d1和d2,当d1-d2的值取最大时,点E的坐标为($\frac{2}{5}$,$\frac{6}{5}$).
如图,二次函数y=-$\frac{1}{2}$(x+2)(x-1)图象与坐标轴的交点分别为A,B,C三点,点E是射线CB上第一象限内一点,记点C、B到直线AE的距离分别为d1和d2,当d1-d2的值取最大时,点E的坐标为($\frac{2}{5}$,$\frac{6}{5}$).
分析 首先说明当AE⊥BC时,d1-d2的值最大,最大值为BC的长.求出直线BC、AE的解析式,利用方程组求出交点E的坐标即可.
解答 解:如图作BM⊥AE于M,CN⊥AE于N,BG⊥CN于G.则四边形BMNG是矩形.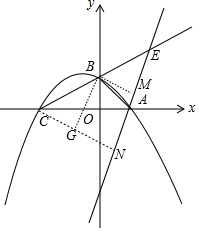
∵d1-d2=CN-BM=CN-NG=CG,
在Rt△BCG中,CG≤BC,
∴当AE⊥BC时,d1-d2的值最大,最大值为BC的长.
由题意C(-2,0),A(1,0),B(0,1),
∴直线BC的解析式为y=$\frac{1}{2}$x+1,
∵AE⊥BC,
∴直线AE的解析式为y=-2x+2,
由$\left\{\begin{array}{l}{y=-2x+2}\\{y=\frac{1}{2}x+1}\end{array}\right.$解得$\left\{\begin{array}{l}{x=\frac{2}{5}}\\{y=\frac{6}{5}}\end{array}\right.$,
∴点E的坐标为($\frac{2}{5}$,$\frac{6}{5}$).
故答案为($\frac{2}{5}$,$\frac{6}{5}$).
点评 本题考查抛物线与x轴的交点、一次函数的应用、最短问题等知识,解题的关键是学会添加常用辅助线,学会构建一次函数,利用方程组确定两个函数的交点坐标.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
10.不等式x+1≥2的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
9.方程x(x2+5x-6)-x(5x+4)=x3-5的解是( )
| A. | x=2 | B. | x=-2 | C. | x=$\frac{1}{2}$ | D. | x=-$\frac{1}{2}$ |
6.下列运算不正确的是( )
| A. | (a5)2=a10 | B. | b7÷b3=b4 | C. | 2a2•(-3a3)=-6a5 | D. | b5•b5=b25 |
 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,若AD=4,∠AOD=60°,求AB的长.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,若AD=4,∠AOD=60°,求AB的长.
 如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿直线AD翻折,使得点C落在点E的位置,BC=6;求线段BE的长.
如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿直线AD翻折,使得点C落在点E的位置,BC=6;求线段BE的长. 如图,在菱形ABCD中,对角线AC和BD交于点O,分别过点B、C作BE∥AC,CE∥BD,BE与CE交于点E.
如图,在菱形ABCD中,对角线AC和BD交于点O,分别过点B、C作BE∥AC,CE∥BD,BE与CE交于点E.