题目内容
13. 如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿直线AD翻折,使得点C落在点E的位置,BC=6;求线段BE的长.
如图,已知AD是△ABC的中线,∠ADC=45°,把△ADC沿直线AD翻折,使得点C落在点E的位置,BC=6;求线段BE的长.
分析 根据翻转变换的性质得到∠EDA=∠CDA=45°,ED=CD,得到∠EDB=90°,根据勾股定理计算即可.
解答 解:由题意可知∠EDA是由∠CDA 翻折得到,
∴∠EDA=∠CDA=45°,ED=CD,
∴∠EDB=90°,
∵AD是△ABC的中线,BC=6,
∴BD=CD=3.
∴ED=BD=3,
在Rt△BDE中,根据勾股定理可得,$BE=\sqrt{B{D^2}+D{E^2}}=\sqrt{9+9}=3\sqrt{2}$.
点评 本题考查的是翻转变换的性质以及勾股定理的应用,翻转变换是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
1. 如图所示,用不等式表示数轴上的解集,正确的是( )
如图所示,用不等式表示数轴上的解集,正确的是( )
 如图所示,用不等式表示数轴上的解集,正确的是( )
如图所示,用不等式表示数轴上的解集,正确的是( )| A. | x<-3或x>3 | B. | -3<x≤1 | C. | -3≤x<1 | D. | x≤-3或x>1 |
2.下列方程中,没有实数根的是( )
| A. | 2x+3=0 | B. | x2-1=0 | C. | $\frac{1}{x-2}$=$\frac{1-x}{2-x}$-3 | D. | x2+x-1=0 |
3.式子4x2-12x+k是一个完全平方式,则常数k等于( )
| A. | 1.5 | B. | 3 | C. | 2.25 | D. | 9 |
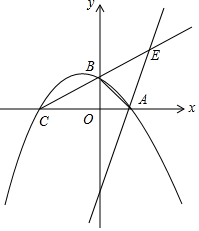 如图,二次函数y=-$\frac{1}{2}$(x+2)(x-1)图象与坐标轴的交点分别为A,B,C三点,点E是射线CB上第一象限内一点,记点C、B到直线AE的距离分别为d1和d2,当d1-d2的值取最大时,点E的坐标为($\frac{2}{5}$,$\frac{6}{5}$).
如图,二次函数y=-$\frac{1}{2}$(x+2)(x-1)图象与坐标轴的交点分别为A,B,C三点,点E是射线CB上第一象限内一点,记点C、B到直线AE的距离分别为d1和d2,当d1-d2的值取最大时,点E的坐标为($\frac{2}{5}$,$\frac{6}{5}$).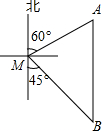 如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.
如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处. 平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.