题目内容
9. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,若AD=4,∠AOD=60°,求AB的长.
如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且AC=BD,若AD=4,∠AOD=60°,求AB的长.
分析 首先证明四边形ABCD是矩形,得出AO=BO=CO=OD,证出△AOD是等边三角形,得出OD=AD=4,求出BD=8,再由勾股定理求出AB即可.
解答 解:∵四边形ABCD是平行四边形,AC=BD,
∴四边形ABCD是矩形,
∴∠BAD=90°,AO=BO=CO=OD,
∵∠AOD=60°,
∴△AOD是等边三角形,
∴DO=AD=4,
∴BD=2OD=8.
在Rt△ABD中,AB=$\sqrt{B{D}^{2}-A{D}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$.
点评 本题考查了矩形的性质,等边三角形的判定与性质,熟记各性质并判断出△AOB是等边三角形是解题的关键.

练习册系列答案
相关题目
1. 如图所示,用不等式表示数轴上的解集,正确的是( )
如图所示,用不等式表示数轴上的解集,正确的是( )
 如图所示,用不等式表示数轴上的解集,正确的是( )
如图所示,用不等式表示数轴上的解集,正确的是( )| A. | x<-3或x>3 | B. | -3<x≤1 | C. | -3≤x<1 | D. | x≤-3或x>1 |
 如图,AB是⊙O的直径,弦CD与AB交于点E,过点B的切线BP与CD的延长线交于点P,连接OC,CB.
如图,AB是⊙O的直径,弦CD与AB交于点E,过点B的切线BP与CD的延长线交于点P,连接OC,CB.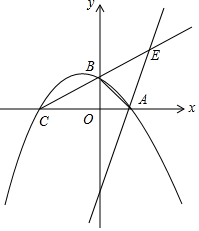 如图,二次函数y=-$\frac{1}{2}$(x+2)(x-1)图象与坐标轴的交点分别为A,B,C三点,点E是射线CB上第一象限内一点,记点C、B到直线AE的距离分别为d1和d2,当d1-d2的值取最大时,点E的坐标为($\frac{2}{5}$,$\frac{6}{5}$).
如图,二次函数y=-$\frac{1}{2}$(x+2)(x-1)图象与坐标轴的交点分别为A,B,C三点,点E是射线CB上第一象限内一点,记点C、B到直线AE的距离分别为d1和d2,当d1-d2的值取最大时,点E的坐标为($\frac{2}{5}$,$\frac{6}{5}$).