题目内容
10. 如图,在菱形ABCD中,对角线AC和BD交于点O,分别过点B、C作BE∥AC,CE∥BD,BE与CE交于点E.
如图,在菱形ABCD中,对角线AC和BD交于点O,分别过点B、C作BE∥AC,CE∥BD,BE与CE交于点E.(1)求证:四边形OBEC是矩形;
(2)当∠ABD=60°,AD=2$\sqrt{3}$时,求∠EDB的正切值.
分析 (1)先依据平行四边形的定义证明四边形OBEC为平行四边形,然后再依据矩形的性质得到∠COB=90°,故此四边形OBEC是矩形;
(2)依据有一个角为60°的等腰三角形是等边三角形可得到BD=2$\sqrt{3}$,然后利用特殊锐角三角函数值可求得AO的长,从而得到BE的长,最后利用锐角三角函数的定义求解即可.
解答 解:(1)∵BE∥AC,CE∥BD,
∴四边形OBEC为平行四边形.
∵ABCD为菱形,
∴AC⊥BD.
∴∠BOC=90°.
∴四边形OBEC是矩形.
(2)∵AD=AB,∠DAB=60°,
∴△ABD为等边三角形.
∴BD=AD=AB=2$\sqrt{3}$.
∵ABCD为菱形,∠DAB=60°,
∴∠BAO=30°.
∴OC=OA=3.
∴BE=3
∴tan∠EDB=$\frac{BE}{BD}$=$\frac{3}{2\sqrt{3}}$=$\frac{\sqrt{3}}{2}$.
点评 本题主要考查的是矩形的判定、菱形的性质、锐角三角函数的定义、特殊锐角三角函数值,熟练掌握相关图形的性质是解题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
2.下列方程中,没有实数根的是( )
| A. | 2x+3=0 | B. | x2-1=0 | C. | $\frac{1}{x-2}$=$\frac{1-x}{2-x}$-3 | D. | x2+x-1=0 |
 如图,AB是⊙O的直径,弦CD与AB交于点E,过点B的切线BP与CD的延长线交于点P,连接OC,CB.
如图,AB是⊙O的直径,弦CD与AB交于点E,过点B的切线BP与CD的延长线交于点P,连接OC,CB.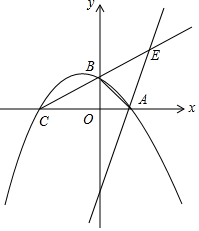 如图,二次函数y=-$\frac{1}{2}$(x+2)(x-1)图象与坐标轴的交点分别为A,B,C三点,点E是射线CB上第一象限内一点,记点C、B到直线AE的距离分别为d1和d2,当d1-d2的值取最大时,点E的坐标为($\frac{2}{5}$,$\frac{6}{5}$).
如图,二次函数y=-$\frac{1}{2}$(x+2)(x-1)图象与坐标轴的交点分别为A,B,C三点,点E是射线CB上第一象限内一点,记点C、B到直线AE的距离分别为d1和d2,当d1-d2的值取最大时,点E的坐标为($\frac{2}{5}$,$\frac{6}{5}$).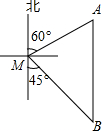 如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处.
如图,一艘渔船位于码头M的南偏东45°方向,距离码头120海里的B处,渔船从B处沿正北方向航行一段距离后,到达位于码头北偏东60°方向的A处. 平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.
平行四边形ABCD中,对角线AC、BD交于点O.M为AD中点,连接CM交BD于点N,且ON=1.