题目内容
18.甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
分析 (1)直接利用概率公式求得概率即可;
(2)利用概率的意义分别分析后即可判断谁的说法正确;
(3)列表将所有等可能的结果列举出来,利用概率公式求解即可.
解答 解:(1)出现向上点数为6的频率=$\frac{1}{6}$;
(2)丙的说法不正确,
理由:(1)因为实验次数较多时,向上点数为6的频率接近于概率,但不说明概率就等一定等于频率;
(2)从概率角度来说,向上点数为6的概率是$\frac{1}{6}$的意义是指平均每6次出现1次;
(3)用表格列出所有等可能性结果:
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
∴P(点数之和为3的倍数)=$\frac{12}{36}$=$\frac{1}{3}$.
点评 本题考查了概率公式和概率的意义、利用频率估计概率的知识,由于骰子是均匀的,与试验次数无关.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
9.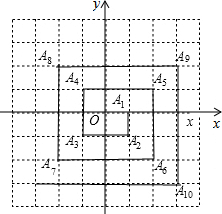 如图,已知A1(1,0),A2(1,1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2010的坐标是( )
如图,已知A1(1,0),A2(1,1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2010的坐标是( )
 如图,已知A1(1,0),A2(1,1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2010的坐标是( )
如图,已知A1(1,0),A2(1,1),A3(-1,-1),A4(-1,1),A5(2,1),…则点A2010的坐标是( )| A. | (502,502) | B. | (-501,-501) | C. | (503,-503) | D. | (-501,501) |
6.给定下列图形可以确定一个圆的是( )
| A. | 已知圆心 | B. | 已知半径 | C. | 已知直径 | D. | 三个点 |
10.在平面直角坐标系中,点M(6,-3)关于x轴对称的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
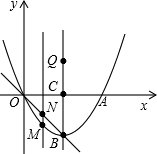 如图,抛物线y=ax2+bx与x轴交于点A,其顶点B在直线l:y=-x上,抛物线的对称轴与x轴交于点C(2,0).
如图,抛物线y=ax2+bx与x轴交于点A,其顶点B在直线l:y=-x上,抛物线的对称轴与x轴交于点C(2,0).
 “奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BC=CD=20m.
“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C地在A地北偏东75°方向.且BC=CD=20m.