题目内容
8.若$y=\sqrt{3-5x}+\sqrt{5x-3}+5$,则xy=3.分析 根据平方数非负数的性质列式求出x,再求出y,然后求出xy.
解答 解:由题意得,3-5x≥0且5x-3≥0,
所以,3-5x=0,
解得x=$\frac{3}{5}$
所以y=5,
所以,xy=$\frac{3}{5}$×5=3,
故答案是:3.
点评 考查了二次根式的意义和性质.概念:式子$\sqrt{a}$(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.同时考查了非负数的性质,几个非负数的和为0,这几个非负数都为0.

练习册系列答案
相关题目
18.在下列给出的条件中,不能判定四边形ABCD一定是平行四边形的是( )
| A. | AB=CD,AD=BC | B. | AB∥CD,AD=BC | C. | AB∥CD,AB=CD | D. | AB∥CD,AD∥BC |
20.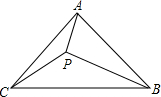 如图,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,且PA=1,PB=3,PC=$\sqrt{7}$,则∠CPA=( )
如图,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,且PA=1,PB=3,PC=$\sqrt{7}$,则∠CPA=( )
 如图,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,且PA=1,PB=3,PC=$\sqrt{7}$,则∠CPA=( )
如图,在等腰Rt△ABC中,∠CAB=90°,P是△ABC内一点,且PA=1,PB=3,PC=$\sqrt{7}$,则∠CPA=( )| A. | 120° | B. | 135° | C. | 150° | D. | 145° |
17.下列命题:(1)一组对边平行的四边形是平行四边形(2)一条对角线平分一个内角的平行四边形是菱形(3)两条对角线互相垂直的矩形是正方形(4)顺次连接对角线相等的四边形各边中点所得的四边形是矩形.其中正确命题的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
| 向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
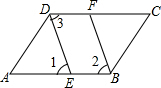 已知:如图,∠ABC=∠ADC,BF、DE是∠ABC、∠ADC的角平分线,DE∥BF.DC和AB有什么位置关系,并加以说明.
已知:如图,∠ABC=∠ADC,BF、DE是∠ABC、∠ADC的角平分线,DE∥BF.DC和AB有什么位置关系,并加以说明.