题目内容
18. 如图,⊙O的直径AB=4,AC=AD,∠CAB=30°,点O到CD的距离OE=$\sqrt{2}$.
如图,⊙O的直径AB=4,AC=AD,∠CAB=30°,点O到CD的距离OE=$\sqrt{2}$.
分析 连接OC,在等腰△ACD中,顶角∠A=30°,易求得∠ACD=75°;根据等边对等角,可得:∠OCA=∠A=30°,由此可得∠OCD=45°,即△COE是等腰直角三角形,则OE=$\sqrt{2}$.
解答 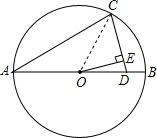 解:连接OC,
解:连接OC,
∵AC=AD,∠CAB=30°,
∴∠ACD=∠ADC=75°.
∵AO=OC,
∴∠OCA=∠CAB=30°;
∴∠OCD=45°,即△OCE是等腰直角三角形.
在等腰Rt△OCE中,
∵OC=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2;
∴OE=OC•sin45°=$\sqrt{2}$,即点O到CD的距离OE等于$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查的是垂径定理,等腰三角形的性质、三角形的内角和定理、解直角三角形等知识的应用,此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
6.我们将宽与长的比是黄金比的矩形称为黄金矩形.已知矩形ABCD是黄金矩形且长AB=10,则宽BC为( )
| A. | 2$\sqrt{5}$-2 | B. | 5$\sqrt{5}$-5 | C. | 15-5$\sqrt{5}$ | D. | 0.618 |
13.用一条长40cm的绳子怎样围成一个面积为75cm2的矩形?设矩形的一边为x米,根据题意,可列方程为( )
| A. | x(40-x)=75 | B. | x(20-x)=75 | C. | x(x+40)=75 | D. | x(x+20)=75 |
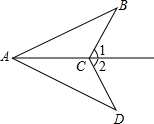 如图,已知△ABC≌△ADC,∠1=64°,则∠2的度数是64°.
如图,已知△ABC≌△ADC,∠1=64°,则∠2的度数是64°.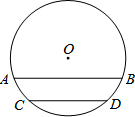 如图,圆柱形油槽内原有积油的水平面宽CD=60cm,油深为10cm.若油面上升10cm,则此时油面宽AB为多少?(教材124页第10题改编)
如图,圆柱形油槽内原有积油的水平面宽CD=60cm,油深为10cm.若油面上升10cm,则此时油面宽AB为多少?(教材124页第10题改编) 如图,⊙0的半径为5cm,点O到直线1的距离OD=3cm,l与⊙O相交于A、B两点,则线段AB上到点O的距离为整数的点有5个.
如图,⊙0的半径为5cm,点O到直线1的距离OD=3cm,l与⊙O相交于A、B两点,则线段AB上到点O的距离为整数的点有5个.