题目内容
18.求下列各式中x的值.(1)x2=5
(2)x2-5=$\frac{4}{9}$
(3)(x-2)2=125
(4)(y+3)3+64=0.
分析 (1)利用数的开方解答;
(2)先移项,然后利用数的开方解答;
(3)是(x+a)2=b的形式,利用数的开方解答;
(4)先移项,写成(x+a)3=b的形式,然后利用数的开方解答.
解答 解:(1)x2=5,
解得x1=$\sqrt{5}$,x2=-$\sqrt{5}$.
(2)x2-5=$\frac{4}{9}$,
x2=$\frac{49}{9}$,
解得x1=$\frac{7}{3}$,x2=-$\frac{7}{3}$.
(3)(x-2)2=125
x-2=±5$\sqrt{5}$,
解得x1=2+5$\sqrt{5}$,x2=2-5$\sqrt{5}$.
(4)(y+3)3+64=0,
(y+3)3=-64,
y+3=-4,
y=-7.
点评 考查了解一元二次方程-直接开平方法,注意
(1)用直接开方法求一元二次方程的解的类型有:x2=a(a≥0);ax2=b(a,b同号且a≠0);(x+a)2=b(b≥0);a(x+b)2=c(a,c同号且a≠0).
法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”.
(2)运用整体思想,会把被开方数看成整体.
(3)用直接开方法求一元二次方程的解,要仔细观察方程的特点.

练习册系列答案
相关题目
11.以a,b,c为边长的下列三角形,能判定是直角三角形的有( )
①a:b:c=1:1:$\sqrt{2}$;
②a,b,c满足a2-b2=c2;
③a=m2+n2,b=mn,c=m2-n2(m>n>0);
④a=1,b=2,c=$\sqrt{3}$.
①a:b:c=1:1:$\sqrt{2}$;
②a,b,c满足a2-b2=c2;
③a=m2+n2,b=mn,c=m2-n2(m>n>0);
④a=1,b=2,c=$\sqrt{3}$.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.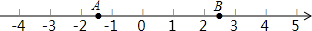 如图,数轴上两点A、B表示的数可能是( )
如图,数轴上两点A、B表示的数可能是( )
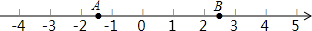 如图,数轴上两点A、B表示的数可能是( )
如图,数轴上两点A、B表示的数可能是( )| A. | -1.5和2.5 | B. | -2.5和2.5 | C. | -1.5和3.5 | D. | -2.5和3.5 |
7. 如图,E、F分别是矩形ABCD边AD、BC上的点,连接AF、CE,恰有∠BFA=∠DEC,则AF与CE的位置关系是( )
如图,E、F分别是矩形ABCD边AD、BC上的点,连接AF、CE,恰有∠BFA=∠DEC,则AF与CE的位置关系是( )
 如图,E、F分别是矩形ABCD边AD、BC上的点,连接AF、CE,恰有∠BFA=∠DEC,则AF与CE的位置关系是( )
如图,E、F分别是矩形ABCD边AD、BC上的点,连接AF、CE,恰有∠BFA=∠DEC,则AF与CE的位置关系是( )| A. | 互相平行 | B. | 互相垂直 | C. | 不相交也不平行 | D. | 无法确定 |
 如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.