题目内容
10. 如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.
如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.(1)求证:点A与C关于直线BD对称.
(2)若∠ADC=90°,求证四边形MPND为正方形.
分析 (1)首先根据角平分线的定义求出∠ABD=∠CBD,然后在△ABD和△CBD中,根据SAS证明两个三角形全等,进而得到∠ADB=∠CDB,AD=CD,根据等腰三角形的性质可得BD垂直平分AC,进而可得点A与C关于直线BD对称;
(2)首先证明四边形PMDN是矩形,再根据角平分线上的点到角两边的距离相等可得PM=PN,进而可得四边形MPND为正方形.
解答 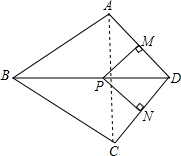 证明:(1)连接AC,
证明:(1)连接AC,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
在△ABD和△CBD中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠DCB}\\{BD=BD}\end{array}\right.$,
∴△ABD≌△CBD(SAS),
∴∠ADB=∠CDB,DA=DC,
∴BD垂直平分AC,
∴点A与C关于直线BD对称;
(2)∵PM⊥AD,PN⊥CD,
∴∠PMD=∠PND=90°,
∵∠ADC=90°,
∴四边形PMDN是矩形,
∵∠ADB=∠CDB,
∴BD平分∠ADC,
∵PM⊥AD,PN⊥CD,
∴PM=PN,
∴四边形MPND为正方形.
点评 此题主要考查了正方形的判定,以及等腰三角形的性质,关键是掌握等腰三角形三线合一,邻边相等的矩形是正方形.

练习册系列答案
相关题目
3.若$\sqrt{x-2y+9}$与|x-y+3|互为相反数,则x+y的值为( )
| A. | 3 | B. | 9 | C. | 12 | D. | 27 |
15.下列说法中,不正确的是( )
| A. | 为了了解一批汽车轮胎的使用年限,应采用抽样调查的方式 | |
| B. | “50名同学中恰有2名同学的生日是同一天”属于随机事件 | |
| C. | “早晨的太阳从东方升起”属于必然事件 | |
| D. | “长为3cm,5cm,9cm的三条线段围成一个三角形”属于可能事件 |
2.娇兰佳人化妆品店为了激发消费者消费,在劳动节当天,对MG面膜进行促销,方案如下:
根据上表中提供的信息,解答下列问题:
(1)若张女士欲购买这款面膜14贴,求她应支付的钱数;
(2)设张女士购买的面膜的数量为x贴,应支付的钱数为y元,请写出y关于x的函数关系式;
(3)若张女士购买面膜的数量为20贴,支付的钱数为y元,当y<170时,求m的取值范围.
| 购买数量(贴) | 单价(元/贴) |
| 不超过10贴(包含10贴) | 9 |
| 超过10贴不超过m贴的部分(15≤m≤30) | 8 |
| 超过m贴的部分 | 7 |
(1)若张女士欲购买这款面膜14贴,求她应支付的钱数;
(2)设张女士购买的面膜的数量为x贴,应支付的钱数为y元,请写出y关于x的函数关系式;
(3)若张女士购买面膜的数量为20贴,支付的钱数为y元,当y<170时,求m的取值范围.
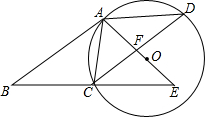 如图,在?ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交干E.
如图,在?ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交干E.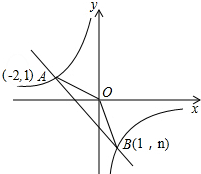 如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的图象交于A(-2,1),B(1,n)两点.
如图,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的图象交于A(-2,1),B(1,n)两点.