题目内容
7.已知(x+$\frac{1}{4}$)2+|y+$\frac{1}{2}$|+(-1)2017=-12016,求4xy-[(x2+5xy-y2)-(x2+3xy-2y2)]的值.分析 利用非负数的性质求出x与y的值,代入原式,去括号合并即可得到结果
解答 解:(x+$\frac{1}{4}$)2+|y+$\frac{1}{2}$|+(-1)2017=-12016,得
x+$\frac{1}{4}$=0,y+$\frac{1}{2}$=0.
解得x=-$\frac{1}{4}$,y=-$\frac{1}{2}$.
原式=4xy-[x2+5xy-y2-x2-3xy+2y2]
=4xy-2xy-y2
=2xy-y2,
当x=-$\frac{1}{4}$,y=-$\frac{1}{2}$时,原式=2×(-$\frac{1}{4}$)×(-$\frac{1}{2}$)-(-$\frac{1}{2}$)2
=$\frac{1}{4}$-$\frac{1}{4}$
=0.
点评 此题考查了整式的加减-化简求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.问题背景:表是某通讯公司推出的移动电话两种计费方式:
若设一个月内用移动电话主叫为t分(t为正整数),根据主叫时间t分析并选择省钱的计费方式.
分析说明:由上表可知,计费与主叫时间相关,计费时首先要看主叫是否超过限定时间.因此,考虑t的取值时,两个主叫限定时间150分和350分是不同时间范围的划分点.
列表解析:当t在不同时间范围内取值时,方式一和方式二的计费如表:(用含t的代数式将表填写完整)
探索比较:由以上分析可知,计费随着主叫时间的变化而变化,比较如下:
①当t小于或等于150分时,因为58<88,所以按方式一的计费少;
②当t大于150且小于350时,方式一的计费由58元增加到108元,而方式二的计费一直是88元,故可能存在某主叫时间按方式一和方式二的计费相等,请你列方程给予解答说明.
③当t=350时,因为108>88,所以按方式二的计费较少;
④当t大于350时,由上表可以看出,方式一的计费为108元加上超过350分部分的超时费,方式二的计费为88元加上超过350分部分的超时费,所以按方式二的计费少.
归纳发现:综合上述分析,可以发现:
主叫时间小于270分时,选择方式一省钱;
主叫时间大于270分时,选择方式二省钱.
| 月使用费/元 | 主叫限定时间/分 | 主叫超时费/(元/分) | 被叫 | |
| 方式一 | 58 | 150 | 0.25 | 免费 |
| 方式二 | 88 | 350 | 0.19 | 免费 |
分析说明:由上表可知,计费与主叫时间相关,计费时首先要看主叫是否超过限定时间.因此,考虑t的取值时,两个主叫限定时间150分和350分是不同时间范围的划分点.
列表解析:当t在不同时间范围内取值时,方式一和方式二的计费如表:(用含t的代数式将表填写完整)
| 主叫时间t/分 | 方式一计费/元 | 方式二计费/元 |
| t小于150 | 58 | 88 |
| t=150 | 58 | 88 |
| t大于150且小于350 | 58+0.25(t-150) | 88 |
| t=350 | 108 | 88 |
| t大于350 | 108+0.25(t-350) | 88+0.19(t-350) |
①当t小于或等于150分时,因为58<88,所以按方式一的计费少;
②当t大于150且小于350时,方式一的计费由58元增加到108元,而方式二的计费一直是88元,故可能存在某主叫时间按方式一和方式二的计费相等,请你列方程给予解答说明.
③当t=350时,因为108>88,所以按方式二的计费较少;
④当t大于350时,由上表可以看出,方式一的计费为108元加上超过350分部分的超时费,方式二的计费为88元加上超过350分部分的超时费,所以按方式二的计费少.
归纳发现:综合上述分析,可以发现:
主叫时间小于270分时,选择方式一省钱;
主叫时间大于270分时,选择方式二省钱.
 求抛物线y=x2-2x的对称轴和顶点坐标,并画出图象.
求抛物线y=x2-2x的对称轴和顶点坐标,并画出图象. 算筹是我国古代的计算工具之一,也是中华民族智慧的结晶,如图1中用算筹表示的算式是“7408+2366”,则图2中算筹表示的算式的运算结果为-426.
算筹是我国古代的计算工具之一,也是中华民族智慧的结晶,如图1中用算筹表示的算式是“7408+2366”,则图2中算筹表示的算式的运算结果为-426.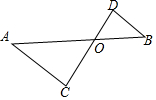 如图,已知△OAC∽△OBD,OA=4,AC=2,OB=2,∠C=∠D.求:
如图,已知△OAC∽△OBD,OA=4,AC=2,OB=2,∠C=∠D.求: 如图,在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
如图,在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.