题目内容
19. 如图,在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.
如图,在△ABC中,AB=AC,点D是BC的中点,点E是AD上任意一点.(1)如图1,连接BE、CE,求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC于F,当∠BAC=45°时,EF=CF;请证明你的结论.
分析 (1)根据等腰三角形的性质就可以求出∠BAE=∠CAE,再证明△ABE≌△ACE就可以得出结论;
(2)由BF⊥AC,∠BAC=45°就可以求出AF=BF,在由条件证明△AEF≌△BCF就可以得出结论.
解答 证明:(1)∵AB=AC,D是BC的中点,
∴∠EAB=∠EAC,
在△ABE和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠EAB=∠EAC}\\{AE=AE}\end{array}\right.$,
∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)当∠BAC=45°时,EF=CF.
∵BF⊥AF,
∴∠AFB=∠CFB=90°.
∵∠BAC=45°,
∴∠ABF=45°,
∴∠ABF=∠BAC,
∴AF=BF.
∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∴∠EAF+∠C=90°,
∵BF⊥AC,
∴∠CBF+∠C=90°,
∴∠EAF=∠CBF,
在△AEF和△BCF中,
$\left\{\begin{array}{l}{∠EAF=∠CBF}\\{AF=BF}\\{∠AFE=∠BFC=90°}\end{array}\right.$,
∴△AEF≌△BCF(ASA)
∴EF=CF.
故答案为:CF.
点评 本题考查了中点的性质的运用,全等三角形的判定性质的运用,等腰三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
4.已知⊙O的半径为8cm,直线l上有一点B到圆心O的距离等于8cm,则直线l与⊙O的位置关系是( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 相交或相切 |
 如图中的三角形为直角三角形,字母A所在的正方形的面积是16.
如图中的三角形为直角三角形,字母A所在的正方形的面积是16.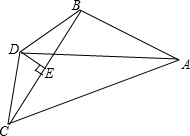 如图,在△ABC中,AC>AB,AD平分∠BAC,点D到点B与点C的距离相等,过点D作DE⊥BC于点E.
如图,在△ABC中,AC>AB,AD平分∠BAC,点D到点B与点C的距离相等,过点D作DE⊥BC于点E.