题目内容
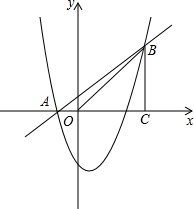 如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)点M是抛物线上的一个点,直线MN平行于y轴交直线AB于N,如果以M、N、B、C为顶点的四边形是平行四边形,求出点M的横坐标.
考点:二次函数综合题
专题:
分析:(1)将A(-1,0)、B(4,5)分别代入y=x2+bx+c求出b和c的值即可;
(2)过点O作OH⊥AB,垂足为H,根据勾股定理可求出AB的长,进而得到:在Rt△BOH中,tan∠ABO=
=
×
=
.
(3)设点M的坐标为(x,x2-2x-3),点N的坐标为(x,x+1),在分两种情况:当点M在点N的上方时和当点M在点N的下方时,则四边形NMCB是平行四边形讨论求出符合题意的点M的横坐标即可.
(2)过点O作OH⊥AB,垂足为H,根据勾股定理可求出AB的长,进而得到:在Rt△BOH中,tan∠ABO=
| OH |
| BH |
| ||
| 2 |
| 2 | ||
9
|
| 1 |
| 9 |
(3)设点M的坐标为(x,x2-2x-3),点N的坐标为(x,x+1),在分两种情况:当点M在点N的上方时和当点M在点N的下方时,则四边形NMCB是平行四边形讨论求出符合题意的点M的横坐标即可.
解答:解:(1)将A(-1,0)、B(4,5)分别代入y=x2+bx+c,得
,
解得b=-2,c=-3.
∴抛物线的解析式:y=x2-2x-3.
(2)在Rt△BOC中,OC=4,BC=5.
在Rt△ACB中,AC=AO+OC=1+4=5,
∴AC=BC.
∴∠BAC=45°,AB=
=5
.
如图1,过点O作OH⊥AB,垂足为H.
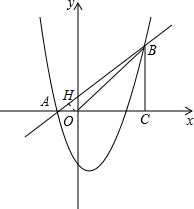
在Rt△AOH中,OA=1,
∴AH=OH=OA×sin45°=1×
=
,
∴BH=AB-AH=5
-
=
,
在Rt△BOH中,tan∠ABO=
=
×
=
.
(3)直线AB的解析式为:y=x+1.
设点M的坐标为(x,x2-2x-3),
点N的坐标为(x,x+1),
①如图2,当点M在点N的上方时,
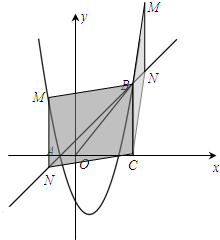
则四边形MNCB是平行四边形,MN=BC=5.
由MN=(x2-2x-3)-(x+1)=x2-2x-3-x-1=x2-3x-4,
解方程x2-3x-4=5,
得x=
或x=
.
②如图3,当点M在点N的下方时,则四边形NMCB是平行四边形,NM=BC=5.

由MN=(x+1)-(x2-2x-3)
=x+1-x2+2x+3=-x2+3x+4,
解方程-x2+3x+4=5,
得x=
或x=
.
所以符合题意的点M有4个,
其横坐标分别为:
,
,
,
.
|
解得b=-2,c=-3.
∴抛物线的解析式:y=x2-2x-3.
(2)在Rt△BOC中,OC=4,BC=5.
在Rt△ACB中,AC=AO+OC=1+4=5,
∴AC=BC.
∴∠BAC=45°,AB=
| AC2+BC2 |
| 2 |
如图1,过点O作OH⊥AB,垂足为H.

在Rt△AOH中,OA=1,
∴AH=OH=OA×sin45°=1×
| ||
| 2 |
| ||
| 2 |
∴BH=AB-AH=5
| 2 |
| ||
| 2 |
9
| ||
| 2 |
在Rt△BOH中,tan∠ABO=
| OH |
| BH |
| ||
| 2 |
| 2 | ||
9
|
| 1 |
| 9 |
(3)直线AB的解析式为:y=x+1.
设点M的坐标为(x,x2-2x-3),
点N的坐标为(x,x+1),
①如图2,当点M在点N的上方时,

则四边形MNCB是平行四边形,MN=BC=5.
由MN=(x2-2x-3)-(x+1)=x2-2x-3-x-1=x2-3x-4,
解方程x2-3x-4=5,
得x=
3+3
| ||
| 2 |
3-3
| ||
| 2 |
②如图3,当点M在点N的下方时,则四边形NMCB是平行四边形,NM=BC=5.

由MN=(x+1)-(x2-2x-3)
=x+1-x2+2x+3=-x2+3x+4,
解方程-x2+3x+4=5,
得x=
3+
| ||
| 2 |
3-
| ||
| 2 |
所以符合题意的点M有4个,
其横坐标分别为:
3+3
| ||
| 2 |
3-3
| ||
| 2 |
3+
| ||
| 2 |
3-
| ||
| 2 |
点评:本题考查了二次函数综合题.其中涉及到的知识点有待定系数法求二次函数的解析式,平行四边形的判定和性质,解一元二次方程以及抛物线的性质以及最值的求解方法.解答(3)题时要分类讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法正确的个数是( )
①同位角相等;
②两条不相交的直线叫做平行线;
③过一点有且只有一条直线与已知直线平行;
④三条直线两两相交,总有三个交点;
⑤若a∥b,b∥c,则a∥c.
①同位角相等;
②两条不相交的直线叫做平行线;
③过一点有且只有一条直线与已知直线平行;
④三条直线两两相交,总有三个交点;
⑤若a∥b,b∥c,则a∥c.
| A、1个 | B、2个 | C、3个 | D、4个 |
下列各图形都是由同样大小的圆和正三角形按一定的规律组成.其中,第①个图形由8个圆和1个正三角形组成,第②个图形由16个圆和4个正三角形组成,第③个图形由24个圆和9个正三角形组成,…则第几个图形中圆和正三角形的个数相等?( )


| A、7 | B、8 | C、9 | D、10 |
下列运算不正确的是( )
| A、a5+a5=2a5 |
| B、(-2a2)2=-4a4 |
| C、2a2•a-1=2a |
| D、(2a3-a2)÷a2=2a-1 |
 已知圆O的直径AB、CD互相垂直,弦AE交CD于F,若圆O的半径为R.求证:AE•AF=2R2.
已知圆O的直径AB、CD互相垂直,弦AE交CD于F,若圆O的半径为R.求证:AE•AF=2R2.
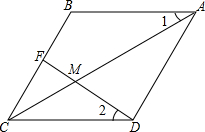 如图,在菱形ABCD中,点M是对角线AC上一点,且MC=MD.连接DM并延长,交边BC于点F.
如图,在菱形ABCD中,点M是对角线AC上一点,且MC=MD.连接DM并延长,交边BC于点F.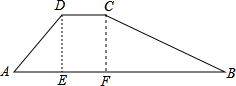 如图,水库大坝截面的迎水坡AD坡比(DE与AE的长度之比)为4:3背水坡BC坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,求大坝的截面面积和周长.
如图,水库大坝截面的迎水坡AD坡比(DE与AE的长度之比)为4:3背水坡BC坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,求大坝的截面面积和周长.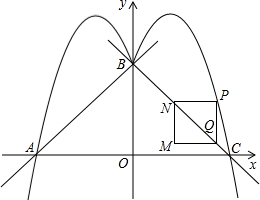 如图,已知抛物线y1=-x2+bx+c(a≤O)与直线AB:y=kx+l交于A(-4,0)、B(0,4);将抛物线y1沿y轴翻折得到抛物线y2且交x轴于点C.
如图,已知抛物线y1=-x2+bx+c(a≤O)与直线AB:y=kx+l交于A(-4,0)、B(0,4);将抛物线y1沿y轴翻折得到抛物线y2且交x轴于点C.