��Ŀ����
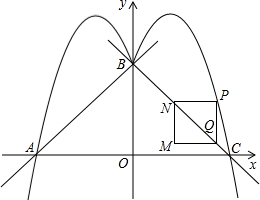 ��ͼ����֪������y1=-x2+bx+c��a��O����ֱ��AB��y=kx+l����A��-4��0����B��0��4������������y1��y�ᷭ�۵õ�������y2�ҽ�x���ڵ�C��
��ͼ����֪������y1=-x2+bx+c��a��O����ֱ��AB��y=kx+l����A��-4��0����B��0��4������������y1��y�ᷭ�۵õ�������y2�ҽ�x���ڵ�C����1����ֱ��AB��������y1�ı���ʽ��
��2����������y2�ı���ʽ��
��3����P��ֱ��BC�Ϸ���������y2�ϵĶ��㣬����P��PQ��x�ύֱ��BC��Q����PQΪ����������PQMN�����P�ĺ�����Ϊm���ú�m�Ĵ���ʽ��ʾPQ�ij����������mΪ��ֵʱ��������PQMN���ܳ����
��4��������ڣ�3���ʵ�ǰ���£���m=1ʱ������E��������y1�ϵĶ��㣬��F��ֱ��AB�ϵĶ��㣬�Ƿ���ڵ�F��ʹ����PQΪ�ߣ���P��Q��E��F������ı���Ϊƽ���ı��Σ������ڣ������F�����ꣻ�������ڣ���˵�����ɣ�
���㣺���κ����ۺ���
ר�⣺
��������1����A��-4��0����B��0��4���ֱ����������y1=-x2+bx+c��a��O����ֱ��AB��y=kx+l�����b��c��k��l��ֵ���ɣ�
��2����Ϊ������y1=-x2+bx+c��a��O����������y2����y��Գƣ�A��-4��0�������Կ����c��ֵ���������a��ֵ������ý⣻
��3�����p��m��-m2+3m+4����Q��m��-m+4������0��m��4��������PQ=��-m2+3m+4��-��-m+4��=-m2+4m������������PQMN���ܳ�=4PQ=-4��m-2��2+16��0��m��4�������ö��κ��������ʼ��ɵõ���mΪ��ֵʱ��������PQMN���ܳ����
��4�����ڣ�����PQΪ��ʱ��Ҫʹ�ı���EFQP��ƽ���ı��Σ�������EF��PQ��EF=PQ����PQΪ��ʱ��Ҫʹ�ı���FEQP��ƽ���ı��Σ�������EF��PQ��EF=PQ�����������F�����꣮
��2����Ϊ������y1=-x2+bx+c��a��O����������y2����y��Գƣ�A��-4��0�������Կ����c��ֵ���������a��ֵ������ý⣻
��3�����p��m��-m2+3m+4����Q��m��-m+4������0��m��4��������PQ=��-m2+3m+4��-��-m+4��=-m2+4m������������PQMN���ܳ�=4PQ=-4��m-2��2+16��0��m��4�������ö��κ��������ʼ��ɵõ���mΪ��ֵʱ��������PQMN���ܳ����
��4�����ڣ�����PQΪ��ʱ��Ҫʹ�ı���EFQP��ƽ���ı��Σ�������EF��PQ��EF=PQ����PQΪ��ʱ��Ҫʹ�ı���FEQP��ƽ���ı��Σ�������EF��PQ��EF=PQ�����������F�����꣮
����⣺��1������֪������y1=-x2+bx+c��a��O����ֱ��AB��y=kx+l����A��-4��0����B��0��4����
��
��
��
��b=-3��k=1��
��y1=-x2-3x+4��AB��y=x+4��
��2����������y1=-x2+bx+c��a��O����������y2����y��Գƣ�A��-4��0����
��C��4��0����a=-1��
��y2=-x2+nx+c��a��O��������y2����C��4��0����
��-16+4n+4=0��
��ã�n=3��
��y2=-x2+3x+4��a��O����
��3����ֱ��BC��y=kx+b����C��4��0����B��0��4����
��ֱ��BC�Ľ���ʽΪy=-x+4��
���p��m��-m2+3m+4����Q��m��-m+4������0��m��4����
��PQ=��-m2+3m+4��-��-m+4��=-m2+4m��
��������PQMN���ܳ�=4PQ=-4��m-2��2+16��0��m��4����
�൱m=2ʱ���ܳ����
��4�����ڣ��������£�
��m=1ʱ��yP=6��yQ=3��
��P��1��6����Q��1��3����PQ=yP-yQ=6-3=3��
��PQΪ��ʱ��Ҫʹ�ı���EFQP��ƽ���ı��Σ�������EF��PQ��EF=PQ��
���E��n��-n2-3n+4����F��n��n+4����n��0����
��EF=��-n2-3n+4��-��n+4����
��-n2-4n=3��
��n=-1��-3��
��F1��-1��3����F2��-3��1����
��PQΪ��ʱ��Ҫʹ�ı���FEQP��ƽ���ı��Σ�������EF��PQ��EF=PQ��
��EF=��n+4��-��-n2-3n+4��=n2+4n��
��n2+4n=3��
��n=-2-
��-2+
����ȥ����
��F3��-2-
��2-
����
�������ڵ�Fʹ���Ե�P��Q��E��FΪ�����ƽ���ı��Σ�
F1��-1��3����F2��-3��1����F3��-2-
��2-
����
��
|
|
��b=-3��k=1��
��y1=-x2-3x+4��AB��y=x+4��
��2����������y1=-x2+bx+c��a��O����������y2����y��Գƣ�A��-4��0����
��C��4��0����a=-1��
��y2=-x2+nx+c��a��O��������y2����C��4��0����
��-16+4n+4=0��
��ã�n=3��
��y2=-x2+3x+4��a��O����
��3����ֱ��BC��y=kx+b����C��4��0����B��0��4����
��ֱ��BC�Ľ���ʽΪy=-x+4��
���p��m��-m2+3m+4����Q��m��-m+4������0��m��4����
��PQ=��-m2+3m+4��-��-m+4��=-m2+4m��
��������PQMN���ܳ�=4PQ=-4��m-2��2+16��0��m��4����
�൱m=2ʱ���ܳ����
��4�����ڣ��������£�
��m=1ʱ��yP=6��yQ=3��
��P��1��6����Q��1��3����PQ=yP-yQ=6-3=3��
��PQΪ��ʱ��Ҫʹ�ı���EFQP��ƽ���ı��Σ�������EF��PQ��EF=PQ��
���E��n��-n2-3n+4����F��n��n+4����n��0����
��EF=��-n2-3n+4��-��n+4����
��-n2-4n=3��
��n=-1��-3��
��F1��-1��3����F2��-3��1����
��PQΪ��ʱ��Ҫʹ�ı���FEQP��ƽ���ı��Σ�������EF��PQ��EF=PQ��
��EF=��n+4��-��-n2-3n+4��=n2+4n��
��n2+4n=3��
��n=-2-
| 7 |
| 7 |
��F3��-2-
| 7 |
| 7 |
�������ڵ�Fʹ���Ե�P��Q��E��FΪ�����ƽ���ı��Σ�
F1��-1��3����F2��-3��1����F3��-2-
| 7 |
| 7 |
�������������ؿ����˴���ϵ��������κ�������ʽ��ƽ���ı��ε��ж������ʵ�֪ʶ�㣬�ۺ���ǿ������ѧ���������ۣ����ν�ϵ���ѧ˼�뷽������2����Ū���߶�ME���ȵĺ��������ǽ���Ĺؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
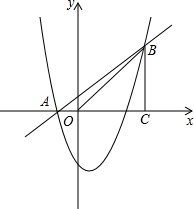 ��ͼ����֪������y=x2+bx+c����A��-1��0����B��4��5�����㣬����B��BC��x�ᣬ����ΪC��
��ͼ����֪������y=x2+bx+c����A��-1��0����B��4��5�����㣬����B��BC��x�ᣬ����ΪC��
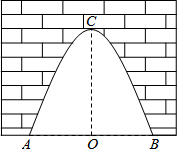 ��ͼ��ij�ų���һ����������ʯ���ţ����ŵ����������AB=4�ף����ŵ����߶�OC=4�ף�
��ͼ��ij�ų���һ����������ʯ���ţ����ŵ����������AB=4�ף����ŵ����߶�OC=4�ף�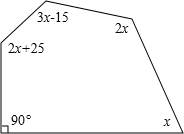 ��ͼ��ʾ���������ͼ����Ϣ���x��ֵ��
��ͼ��ʾ���������ͼ����Ϣ���x��ֵ��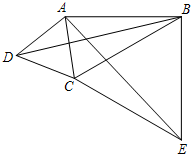 ��ͼ�����ı���ABCD�У���ABC=30�㣬��ADC=60�㣬AD=DC������AC��BD�����ı���ABCD���ⲿ��BCΪһ�����ȱ�������BCE������AE��
��ͼ�����ı���ABCD�У���ABC=30�㣬��ADC=60�㣬AD=DC������AC��BD�����ı���ABCD���ⲿ��BCΪһ�����ȱ�������BCE������AE��