题目内容
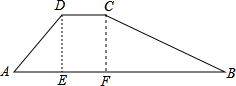 如图,水库大坝截面的迎水坡AD坡比(DE与AE的长度之比)为4:3背水坡BC坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,求大坝的截面面积和周长.
如图,水库大坝截面的迎水坡AD坡比(DE与AE的长度之比)为4:3背水坡BC坡比为1:2,大坝高DE=20m,坝顶宽CD=10m,求大坝的截面面积和周长.考点:解直角三角形的应用-坡度坡角问题
专题:
分析:根据DE=20m,和斜坡AD、BC的坡比,在Rt△ADE和Rt△CBF中分别求出AE、AD和BF、BC的长度,继而可求得大坝的截面面积和周长.
解答:解:∵DE=20m,DE:AE=4:3,
∴AE=15m,
∴AD=
=25m,
∵CE=DE=20m,CF:BF=1:2,
∴BF=40m,
∴BC=
=20
m,
则周长C=AD+DC+BC+AB=(100+25
)m,
面积S=
(DC+AB)•DE=
×75×20=750(m2).
∴AE=15m,
∴AD=
| AE2+DE2 |
∵CE=DE=20m,CF:BF=1:2,
∴BF=40m,
∴BC=
| CF2+BF2 |
| 5 |
则周长C=AD+DC+BC+AB=(100+25
| 5 |
面积S=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了坡度和坡角的知识,解答本题的关键是根据坡比和已知条件求出三角形的边长以及勾股定理的应用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
方程x2-6x+4=0的根的情况( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、不能确定 |
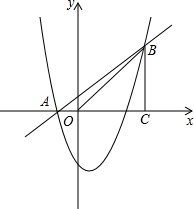 如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.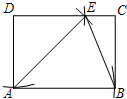 如图,在矩形ABCD中,以点D为圆心,DA长为半径画弧,交CD于点E,以点A为圆心,AE长为半径画弧,恰好经过点B,连结BE、AE.求∠EBC的度数.
如图,在矩形ABCD中,以点D为圆心,DA长为半径画弧,交CD于点E,以点A为圆心,AE长为半径画弧,恰好经过点B,连结BE、AE.求∠EBC的度数.
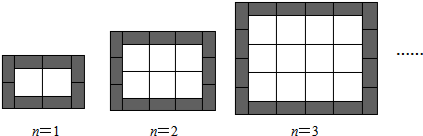
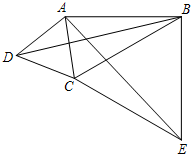 如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连接AC、BD.在四边形ABCD的外部以BC为一边作等边三角形BCE,连接AE.
如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连接AC、BD.在四边形ABCD的外部以BC为一边作等边三角形BCE,连接AE.