题目内容
下列说法正确的个数是( )
①同位角相等;
②两条不相交的直线叫做平行线;
③过一点有且只有一条直线与已知直线平行;
④三条直线两两相交,总有三个交点;
⑤若a∥b,b∥c,则a∥c.
①同位角相等;
②两条不相交的直线叫做平行线;
③过一点有且只有一条直线与已知直线平行;
④三条直线两两相交,总有三个交点;
⑤若a∥b,b∥c,则a∥c.
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:平行公理及推论,相交线,同位角、内错角、同旁内角,平行线
专题:
分析:根据平行线的定义,平行公理和相交线对各小题分析判断利用排除法求解.
解答:解:①∵同位角不一定是两平行直线被截得到,
∴同位角相等错误,故本小题错误;
②应为,在同一平面内两条不相交的直线叫做平行线,故本小题错误;
③过一点有且只有一条直线与已知直线平行,正确;
④三条直线两两相交,总有一个或三个交点,故本小题错误;
⑤若a∥b,b∥c,则a∥c,正确.
综上所述,说法正确的有③⑤共2个.
故选B.
∴同位角相等错误,故本小题错误;
②应为,在同一平面内两条不相交的直线叫做平行线,故本小题错误;
③过一点有且只有一条直线与已知直线平行,正确;
④三条直线两两相交,总有一个或三个交点,故本小题错误;
⑤若a∥b,b∥c,则a∥c,正确.
综上所述,说法正确的有③⑤共2个.
故选B.
点评:本题考查了平行公理,相交线与平行线,同位角的定义,是基础题,熟记概念是解题的关键.

练习册系列答案
相关题目
在方程3x-y=2,x+
=0,
x=
,x2-2x-3=0,2(x2-3x)=x(2x-3)+5中一元一次方程的个数为( )
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列计算正确的是( )
| A、3a-a=2 |
| B、(a2)4=a8 |
| C、a+a4=a5 |
| D、(a+b)(a-b)=a2+b2 |
下列车标图案中,是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
在相同条件下重复试验,若事件A发生的概率是
,下列陈述正确的是( )
| 7 |
| 100 |
| A、说明做100次这种试验,事件A必发生7次 | ||
| B、说明大量反复做这种试验,事件A平均每100次发生7次 | ||
| C、说明做100次这种试验,事件A不可能必发生6次 | ||
D、说明事件A发生的频率是
|
方程x2-6x+4=0的根的情况( )
| A、有两个不相等的实数根 |
| B、有两个相等的实数根 |
| C、没有实数根 |
| D、不能确定 |
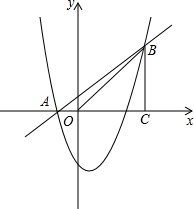 如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
如图,已知抛物线y=x2+bx+c经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.