题目内容
6. 设ABCD是一块正方形纸板,用平行于BC的直线PQ和RS将它等分三个矩形,如图,折叠纸板,使C点落在AB上的C′点处,S点落在PQ的S′点处,且BC′=1,试求AC′的长.
设ABCD是一块正方形纸板,用平行于BC的直线PQ和RS将它等分三个矩形,如图,折叠纸板,使C点落在AB上的C′点处,S点落在PQ的S′点处,且BC′=1,试求AC′的长.
分析 由折叠的性质得到C′E=CE,C′S′=CS,设AC′=x,BE=y,根据勾股定理得到y=$\frac{{x}^{2}+2x}{2(x+1)}$ ①,根据相似三角形的性质得到2x2+x-3xy=1 ②,把①代入②得,即可得到结论.
解答 解:∵C′D′与CD,C′E与CE关于执行EM对称,
∴C′E=CE,C′S′=CS,
设AC′=x,BE=y,
在Rt△BC′E中,y2+1=(x+1-y)2,
∴y=$\frac{{x}^{2}+2x}{2(x+1)}$ ①,
∵△PC′S′∽△BEC′,
∴$\frac{PC′}{BE}$=$\frac{C′S′}{C′E}$,即$\frac{x-\frac{1}{3}(x+1)}{y}$=$\frac{\frac{1}{3}(x+1)}{x+1-y}$,
∴2x2+x-3xy=1 ②,
把①代入②得,2x2+x-3x•$\frac{{x}^{2}+2x}{2(x+1)}$=1,
解得x3=2,
∴x=$\root{3}{2}$,
即AC′的长为$\root{3}{2}$.
点评 本题考查了翻折变换-折叠问题,矩形的性质,相似三角形的判定和性质,勾股定理,熟练掌握折叠的性质是解题的关键.

练习册系列答案
相关题目
17.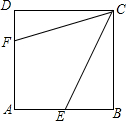 如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若点E为AB的中点,且满足BE+DF=EF,则EF的长为( )
如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若点E为AB的中点,且满足BE+DF=EF,则EF的长为( )
 如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若点E为AB的中点,且满足BE+DF=EF,则EF的长为( )
如图,正方形ABCD的边长为6,点E、F分别在AB,AD上,若点E为AB的中点,且满足BE+DF=EF,则EF的长为( )| A. | 4 | B. | 3$\sqrt{2}$ | C. | 5 | D. | 4$\sqrt{2}$ |
1.已知点A(3,a),B(-1,b),C (-2,c)都在函数y=$\frac{4}{x}$的图象上,则a、b、c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | c>b>a | D. | a>c>b |
11.如果点P(m+3,m+1)在x轴上,则点P的坐标为( )
| A. | (0,2) | B. | (2,0) | C. | (4,0) | D. | (0,-4) |
18. 如图,点P是直线y=$\frac{1}{2}$x+1上动点,点Q(0,m)是y轴负半轴上定点,连接PQ,当PQ的长度最小时,∠PQO的正弦值为( )
如图,点P是直线y=$\frac{1}{2}$x+1上动点,点Q(0,m)是y轴负半轴上定点,连接PQ,当PQ的长度最小时,∠PQO的正弦值为( )
 如图,点P是直线y=$\frac{1}{2}$x+1上动点,点Q(0,m)是y轴负半轴上定点,连接PQ,当PQ的长度最小时,∠PQO的正弦值为( )
如图,点P是直线y=$\frac{1}{2}$x+1上动点,点Q(0,m)是y轴负半轴上定点,连接PQ,当PQ的长度最小时,∠PQO的正弦值为( )| A. | $\frac{{2\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | 和m的取值有关 |
 如图,在△ABC中,∠ACB=90°,点D是AB的中点,且DC=5cm,则AB=10cm.
如图,在△ABC中,∠ACB=90°,点D是AB的中点,且DC=5cm,则AB=10cm. 如图,在平面直角坐标系中,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,抛物线y=$\frac{1}{4}$x2+bx+c经过B(-2,0)、D(6,3)两点.
如图,在平面直角坐标系中,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,抛物线y=$\frac{1}{4}$x2+bx+c经过B(-2,0)、D(6,3)两点.