题目内容
10.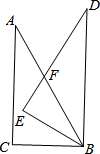 如图,△ABC中,∠C=90°,∠A=30°,AB=8,现将△ABC绕点B顺时针旋转30°至△DEB,DE交AB于点F,求线段DF的长.
如图,△ABC中,∠C=90°,∠A=30°,AB=8,现将△ABC绕点B顺时针旋转30°至△DEB,DE交AB于点F,求线段DF的长.
分析 利用特殊锐角三角函数值可求得BC=4,AC=4$\sqrt{3}$,由旋转的性质可知DE=AC=4$\sqrt{3}$,∠EBF=30°,∠E=90°,EB=BC=4,在△EFB中利用特殊锐角三角函数可求得EF的长,最后根据DF=ED-EF求解即可.
解答 解:∵∠C=90°,∠A=30°,AB=8,
∴∠CBA=60°,CB=4.
∴AC=$\sqrt{3}$CB=4$\sqrt{3}$.
由旋转的性质可知:∠CBE=30°,AC=ED=4$\sqrt{3}$,∠C=∠E=90°.
∴∠EBF=30°.
∴EF=$\frac{\sqrt{3}}{3}EB$=$\frac{4\sqrt{3}}{3}$.
∴DF=DE-EF=$4\sqrt{3}-\frac{4\sqrt{3}}{3}$=$\frac{8\sqrt{3}}{3}$.
点评 本题考查了旋转的性质、特殊锐角三角函数,求得∠E=90°,BE=4,∠EBF=30°是解题的关键.

练习册系列答案
相关题目
20.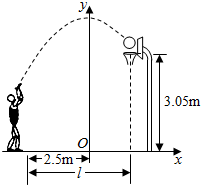 在某次投篮中,球从出手到投中篮圈中心的运动路径是抛物线y=-$\frac{1}{5}$x2+3.5的一部分(如图),则他与篮底的水平距离l(如图)是( )
在某次投篮中,球从出手到投中篮圈中心的运动路径是抛物线y=-$\frac{1}{5}$x2+3.5的一部分(如图),则他与篮底的水平距离l(如图)是( )
 在某次投篮中,球从出手到投中篮圈中心的运动路径是抛物线y=-$\frac{1}{5}$x2+3.5的一部分(如图),则他与篮底的水平距离l(如图)是( )
在某次投篮中,球从出手到投中篮圈中心的运动路径是抛物线y=-$\frac{1}{5}$x2+3.5的一部分(如图),则他与篮底的水平距离l(如图)是( )| A. | 3.5m | B. | 4m | C. | 4.5m | D. | 4.6m |
 如图,在△ABC中,AB=AC,∠C=30°,AD⊥AB交BC于D,AD=3cm,求BC的长.
如图,在△ABC中,AB=AC,∠C=30°,AD⊥AB交BC于D,AD=3cm,求BC的长. 如图,已知线段AB.
如图,已知线段AB.