题目内容
15．
如图，已知线段AB．（1）延长线段AB到C，使BC=2AB，若AB=2cm，求AC的长；
（2）反向延长线段AB到点D，使DA=$\frac{1}{2}$AB，若AB=4cm，求DB的长．
分析 （1）根据BC与AB的关系，可得BC的长，根据线段的和差，可得答案；
（2）根据DA=$\frac{1}{2}$AB，可得DA的长，根据线段的和差，可得答案．
解答 解：（1）由BC=2AB，若AB=2cm，得
BC=2AB=2×2=4cm，
由线段的和差，得
AC=AB+BC=2+4=6cm；
（2）由DA=$\frac{1}{2}$AB，若AB=4cm，得
DA=$\frac{1}{2}$AB=$\frac{1}{2}$×4=2cm，
DB=AD+AB=2+4=6cm．
点评 本题考查了两点间的距离，利用线段BC与AB的关系得出BC的长是解题关键，又利用了线段的和差．
练习册系列答案
相关题目
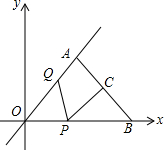已知：如图点A（6，8）在正比例函数图象上，B（12，0），联结AB，AO=AB=10，点C是线段AB的中点，点P在线段BO上以每秒3个单位的速度由B点向O点运动，点Q在线段AO上由A点向O点运动，P、Q两点同时运动，同时停止，运动时间为t秒．
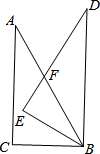如图，△ABC中，∠C=90°，∠A=30°，AB=8，现将△ABC绕点B顺时针旋转30°至△DEB，DE交AB于点F，求线段DF的长．
20．明明借助一副三角尺和量角器，先画∠AOB=90°，再以点O为顶点，OB为始边，作∠BOC=30°，最后作∠AOC的平分线OD，则∠COD的度数为（ ）
| A． | 30° | B． | 60° | C． | 30°或60° | D． | 15°或45° |
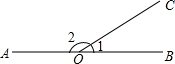如图所示，射线OC将平角AOB分成∠1和∠2两个角．