题目内容
19.已知圆锥的母线长为13cm,侧面展开图的面积为65πcm2,则这个圆锥的高为12cm.分析 设圆锥的底面圆的半径为r,利用圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长和扇形的面积公式得到$\frac{1}{2}$•2π•r•13=65π,解得r=5,然后利用勾股定理计算圆锥的高.
解答 解:设圆锥的底面圆的半径为r,
根据题意得$\frac{1}{2}$•2π•r•13=65π,
解得r=5,
所以圆锥的高=$\sqrt{1{3}^{2}-{5}^{2}}$=12(cm).
故答案为12cm.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
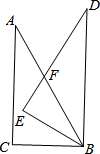 如图,△ABC中,∠C=90°,∠A=30°,AB=8,现将△ABC绕点B顺时针旋转30°至△DEB,DE交AB于点F,求线段DF的长.
如图,△ABC中,∠C=90°,∠A=30°,AB=8,现将△ABC绕点B顺时针旋转30°至△DEB,DE交AB于点F,求线段DF的长.