题目内容
20.当x=-$\frac{1}{5}$,y=1时,求(3x+2y)•(3x-2y)+(x-2y)2的值.分析 直接利用乘法公式将去括号合并同类项,进而将已知代入求出答案.
解答 解:(3x+2y)•(3x-2y)+(x-2y)2
=9x2-4y2+x2+4y2-4xy
=10x2-4xy,
将x=-$\frac{1}{5}$,y=1代入上式得:
原式=10x2-4xy=10×(-$\frac{1}{5}$)2-4×(-$\frac{1}{5}$)×1=$\frac{2}{5}$+$\frac{4}{5}$=$\frac{6}{5}$.
点评 此题主要考查了整式的混合运算,正确合并同类项是解题关键.

练习册系列答案
相关题目
11.抛物线y=-(x+6)(x-4)的顶点坐标是( )
| A. | (-1,25) | B. | (-1,-25) | C. | (1,-21) | D. | (1,21) |
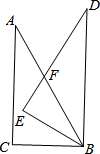 如图,△ABC中,∠C=90°,∠A=30°,AB=8,现将△ABC绕点B顺时针旋转30°至△DEB,DE交AB于点F,求线段DF的长.
如图,△ABC中,∠C=90°,∠A=30°,AB=8,现将△ABC绕点B顺时针旋转30°至△DEB,DE交AB于点F,求线段DF的长.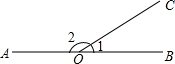 如图所示,射线OC将平角AOB分成∠1和∠2两个角.
如图所示,射线OC将平角AOB分成∠1和∠2两个角. 已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连接ME、MD、ED.
已知:如图,在△ABC中,AD⊥BC,垂足为点D,BE⊥AC,垂足为点E,M为AB边的中点,连接ME、MD、ED.