题目内容
已知M、N是线段AB的垂直平分线上的两点,且∠MBA=60°,∠NBA=15°,先画出图形,再求∠MAN.
考点:线段垂直平分线的性质
专题:
分析:分为两种情况:①当M、N在AB的同旁时,②当M、N在AB的两旁时,分别求出∠MAB和∠NAB的度数,即可得出答案.
解答:解:分为两种情况:①如图1,当M、N在AB的同旁时,
∵M、N是线段AB的垂直平分线上的两点,
∴MA=MB,NA=NB,
∵∠MBA=60°,∠NBA=15°,
∴∠NAB=∠NBA=15°,∠MAB=∠MBA=60°,
∴∠MAN=60°-15°=45°;

②如图2,当M、N在AB的两旁时,
∠MAN=60°+15°=75°.

∵M、N是线段AB的垂直平分线上的两点,
∴MA=MB,NA=NB,
∵∠MBA=60°,∠NBA=15°,
∴∠NAB=∠NBA=15°,∠MAB=∠MBA=60°,
∴∠MAN=60°-15°=45°;

②如图2,当M、N在AB的两旁时,
∠MAN=60°+15°=75°.
点评:本题考查了等腰三角形的性质,线段的垂直平分线性质的应用,用了分类讨论思想,题目比较好,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中错误的是( )
如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,则下列结论中错误的是( )| A、∠COE=∠DOE | ||||
| B、CE=DE | ||||
| C、AE=BE | ||||
D、
|
观察下列图案,既是轴对称图形又是中心对称图形的有( )
A、 |
B、 |
C、 |
D、 |
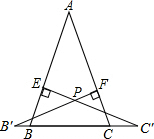 如图,在△ABC中AB=AC,P是△ABC内任意一点,PE⊥AB,PF⊥AC,垂足分别是E、F,且EP、FP的延长线分别交BC所在的直线与点B′、C′.
如图,在△ABC中AB=AC,P是△ABC内任意一点,PE⊥AB,PF⊥AC,垂足分别是E、F,且EP、FP的延长线分别交BC所在的直线与点B′、C′.