题目内容
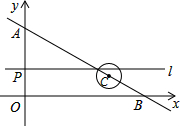
如图,已知平面直角坐标系中,⊙O的圆心在坐标原点,直线l与x轴相交于点P,与⊙O相交于A、B两点,∠AOB=90°.点A和点B的横坐标是方程x2-x-k=0的两根,且两根之差为3.
(1)求方程x2-x-k=0的两根;
(2)求A、B两点的坐标及⊙O的半径;
(3)把直线l绕点P旋转,使直线l与⊙O相切,求直线l的解析式.

(1)求方程x2-x-k=0的两根;
(2)求A、B两点的坐标及⊙O的半径;
(3)把直线l绕点P旋转,使直线l与⊙O相切,求直线l的解析式.

考点:圆的综合题
专题:
分析:(1)设方程的两根分别为x1,x2(x1>x2),根据点A和点B的横坐标是方程x2-x-k=0的两根,且两根之差为3列出方程组
,再求解即可;
(2)过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,先证出△AOC≌△OBD,求出BD=OC=1,AC=OD=2,再求出点A、B的坐标,即可求出OA,
(3)设直线AB的解析式为y=k1x+b1,求出y=-
x+
,当y=0时,求出P的坐标,当直线l与⊙O的切点在第一象限时,设直线l与⊙O相切于点E,过点E作EF⊥x轴于点F,根据OE⊥PE,求出PE,根据S△POE=
OP•EF=
OE•PE,求出EF,从而得出OF=1,E(1,2),设直线l的解析式为y=k2x+b2,则
,
求出y=-
x+
,当直线l与⊙O的切点在第四象限时,同理可求得y=
x-
.
|
(2)过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,先证出△AOC≌△OBD,求出BD=OC=1,AC=OD=2,再求出点A、B的坐标,即可求出OA,
(3)设直线AB的解析式为y=k1x+b1,求出y=-
| 1 |
| 3 |
| 5 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
|
求出y=-
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解答:解:(1)设方程的两根分别为x1,x2(x1>x2),由已知得:
,
解得
,
则方程的两根分别为2和-1;
 (2)过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
(2)过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
在△AOC和△OBD中,
,
∴△AOC≌△OBD(AAS)
∴BD=OC=1,AC=OD=2,
∴A(-1,2),B(2,1),
∴OA=
=
=
,
(3)设直线AB的解析式为y=k1x+b1,则
,
解得
,
∴y=-
x+
,
当y=0时,-
x+
=0,解得x=5,
∴P(5,0),
当直线l与⊙O的切点在第一象限时,设直线l与⊙O相切于点E,过点E作EF⊥x轴于点F,
∵PE是⊙O的切线,
∴OE⊥PE,
∴PE=
=
=2
,
∵S△POE=
OP•EF=
OE•PE,
∴5EF=
•2
,
∴EF=2,
∴OF=
=1,E(1,2),
设直线l的解析式为y=k2x+b2,则
,
解得
,
∴y=-
x+
,
当直线l与⊙O的切点在第四象限时,同理可求得y=
x-
.
|
解得
|
则方程的两根分别为2和-1;
 (2)过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
(2)过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,在△AOC和△OBD中,
|
∴△AOC≌△OBD(AAS)
∴BD=OC=1,AC=OD=2,
∴A(-1,2),B(2,1),
∴OA=
| OC2+AC2 |
| 1+4 |
| 5 |
(3)设直线AB的解析式为y=k1x+b1,则
|
解得
|
∴y=-
| 1 |
| 3 |
| 5 |
| 3 |
当y=0时,-
| 1 |
| 3 |
| 5 |
| 3 |
∴P(5,0),
当直线l与⊙O的切点在第一象限时,设直线l与⊙O相切于点E,过点E作EF⊥x轴于点F,
∵PE是⊙O的切线,
∴OE⊥PE,
∴PE=
| OP2-OE2 |
| 25-5 |
| 5 |
∵S△POE=
| 1 |
| 2 |
| 1 |
| 2 |

∴5EF=
| 5 |
| 5 |
∴EF=2,
∴OF=
| 5-4 |
设直线l的解析式为y=k2x+b2,则
|
解得
|
∴y=-
| 1 |
| 2 |
| 5 |
| 2 |
当直线l与⊙O的切点在第四象限时,同理可求得y=
| 1 |
| 2 |
| 5 |
| 2 |
点评:此题考查了圆的综合,用到的知识点是全等三角形的判定与性质、勾股定理、一次函数、切线的性质,关键是做出辅助线,找出全等三角形,注意分两种情况讨论.

练习册系列答案
相关题目
下列说法正确的是( )
| A、三点确定一个圆 |
| B、正多边形既是轴对称图形也是中心对称图形 |
| C、等弧所对的圆周角相等 |
| D、垂直于半径的直线是圆的切线 |
 如图:在Rt△ABC中,∠C=90°,∠A=22.5°,DC=BC,DE⊥AB,求证:AE=BE.
如图:在Rt△ABC中,∠C=90°,∠A=22.5°,DC=BC,DE⊥AB,求证:AE=BE.
 如图,平面直角坐标系的长度单位是厘米,直线y=-
如图,平面直角坐标系的长度单位是厘米,直线y=-