题目内容
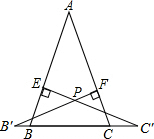 如图,在△ABC中AB=AC,P是△ABC内任意一点,PE⊥AB,PF⊥AC,垂足分别是E、F,且EP、FP的延长线分别交BC所在的直线与点B′、C′.
如图,在△ABC中AB=AC,P是△ABC内任意一点,PE⊥AB,PF⊥AC,垂足分别是E、F,且EP、FP的延长线分别交BC所在的直线与点B′、C′.(1)求证:PB′=PC′;
(2)试一试,若P点在△ABC的外部,其他条件不变,结论是否还成立?若能成立,请给予证明;若不成立,请给出理由.
考点:全等三角形的判定与性质,等腰三角形的性质
专题:
分析:(1)利用等腰三角形的性质得到∠ABC=∠ACB,又PE⊥AB,PF⊥AC,所以可得出∠B′=∠C′,得到PB′=PC′;
(2)结论成立,证明方法类似(1).
(2)结论成立,证明方法类似(1).
解答:(1)证明:∵AB=AC.
∴∠ABC=∠ACB;
又∵PF⊥AC,PEE⊥AB.
∴∠PB'C'=∠PC'B'(等角的余角相等),
∴PB'=PC';
(2)若点P在△ABC外部,其他条件不变,结论仍成立,理由如下:
证明(与上面的证法类似):
∵AB=AC.
∴∠ABC=∠ACB;
又∵PF⊥AC,PE⊥AB.
∴∠PB'C'=∠PC'B'(等角的余角相等),
∴PB'=PC'.
∴∠ABC=∠ACB;
又∵PF⊥AC,PEE⊥AB.
∴∠PB'C'=∠PC'B'(等角的余角相等),
∴PB'=PC';
(2)若点P在△ABC外部,其他条件不变,结论仍成立,理由如下:
证明(与上面的证法类似):
∵AB=AC.
∴∠ABC=∠ACB;
又∵PF⊥AC,PE⊥AB.
∴∠PB'C'=∠PC'B'(等角的余角相等),
∴PB'=PC'.
点评:本题主要考查等腰三角形的判断和性质,由条件得到∠PB'C'=∠PC'B'是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 朋友,你洗过衣服吗?洗衣服后是不是留下了许多不能用的小块肥皂,可别浪费了,你只要把他们放入容器中加点甘油,再加热,小块肥皂很快就可以融化,假如将280g的小肥皂进行融化,使之成为一个正方体状,那么这个正方体的棱长是多少你知道吗?(如图是一块完整的雕牌肥皂)(精确到0.1)(温馨提示:6.3583≈257.04)
朋友,你洗过衣服吗?洗衣服后是不是留下了许多不能用的小块肥皂,可别浪费了,你只要把他们放入容器中加点甘油,再加热,小块肥皂很快就可以融化,假如将280g的小肥皂进行融化,使之成为一个正方体状,那么这个正方体的棱长是多少你知道吗?(如图是一块完整的雕牌肥皂)(精确到0.1)(温馨提示:6.3583≈257.04) 已知△ABC中,∠B=60°,∠A、∠C的平分线AD、CE交于点O.求证:
已知△ABC中,∠B=60°,∠A、∠C的平分线AD、CE交于点O.求证: 看图填空:
看图填空: 如图:在Rt△ABC中,∠C=90°,∠A=22.5°,DC=BC,DE⊥AB,求证:AE=BE.
如图:在Rt△ABC中,∠C=90°,∠A=22.5°,DC=BC,DE⊥AB,求证:AE=BE.