题目内容
4.已知:点A(0,5),B(0,2),在坐标轴上找点C,使△ABC的面积为5,则点C的坐标是($\frac{10}{3}$,0)或(-$\frac{10}{3}$,0).
分析 根据点A、B的坐标求出AB,再利用三角形的面积求出点C到AB的距离,然后分两种情况写出点C的坐标即可.
解答 解:∵A(0,5),B(0,2),
∴AB=5-2=3,
设点C(x,0),
则S△ABC=$\frac{1}{2}$AB•|x|=$\frac{1}{2}$×3•|x|=5,
∴|x|=$\frac{10}{3}$,
∴x=±$\frac{10}{3}$,
点C的坐标为($\frac{10}{3}$,0)或(-$\frac{10}{3}$,0).
故答案为:($\frac{10}{3}$,0)或(-$\frac{10}{3}$,0).
点评 本题考查了坐标与图形性质,三角形的面积,比较简单,根据点A、B的坐标求出AB的长度是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
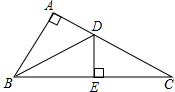 如图,已知Rt△ABC中,AB=AC、BC=10,∠A为Rt∠,BD为△ABC的一条角平分线,过点D作DE垂直于BC,求△CDE的周长.
如图,已知Rt△ABC中,AB=AC、BC=10,∠A为Rt∠,BD为△ABC的一条角平分线,过点D作DE垂直于BC,求△CDE的周长.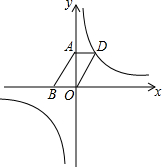 已知反比例函数y=$\frac{1-2m}{x}$(m为常数)的图象在一,三象限.
已知反比例函数y=$\frac{1-2m}{x}$(m为常数)的图象在一,三象限.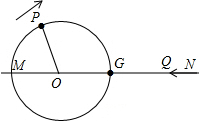

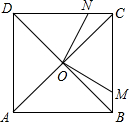 已知四边形ABCD是正方形,M、N分别是边BC、CD上的动点,正方形ABCD的边长为4cm
已知四边形ABCD是正方形,M、N分别是边BC、CD上的动点,正方形ABCD的边长为4cm