题目内容
5.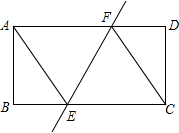 如图,把矩形ABCD沿EF折叠,使点C与点A重合,折痕EF交BC于E,交AD于F,连接AE,CF
如图,把矩形ABCD沿EF折叠,使点C与点A重合,折痕EF交BC于E,交AD于F,连接AE,CF(1)判断四边形AECF的形状,并说明理由;
(2)如果AB=4,AD=8,求:①△ABE的周长;②折痕EF的长.
分析 (1)根据已知条件判定△ABE≌△CDF,进而证明四边形AECFD的四边相等问题得证;
(2)①在Rt△ABE中,利用勾股定理求出BE的长,即可得到△ABE的周长;
②由①的结论在Rt△ABC中求出EO的长,即可得到结论.
解答 证明:(1)四边形AECF是菱形,
根据对折可知,AF=CF,AE=CE,∠EAF=∠ECF,
∵四边形ABCD是矩形,
∴∠B=∠D,AB=CD
∴△ABE≌△CDF,
∴AE=CF,
∴AE=CE=CF=AF,
∴四边形AECF是菱形;
(2)①连接AC交EF于O,设BE=x,则EC=AE=8-x,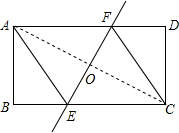
故在Rt△ABE中,(8-x)2=x2+42,
解得x=3,
∴BE=3;
∴AE=5,
∴△ABE的周长=4+3+5=12;
②∵菱形对角线互相平分,
∴AO=CO,
在Rt△ABC中,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$,
∴AO=2$\sqrt{5}$,
EO2=AE2-AO2=52-(2$\sqrt{5}$)2=5,
∴EO=$\sqrt{5}$,
∴EF=2$\sqrt{5}$.
点评 本题主要考查菱形的判定方法:四条边都相等的四边形是菱形和全等三角形的判定方法以及图形的翻折变换(折叠问题)实质上就是轴对称变换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.如果点K、L、M、N分别是四边形ABCD的四条边AB、BC、CD、DA的中点,且四边形KLMN是菱形,那么下列选项正确的是( )
| A. | AB⊥BC | B. | AC⊥BD | C. | AB=BC | D. | AC=BD |
3.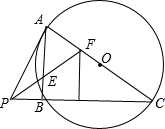 如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
 如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )
如图,已知:PA切⊙O于A,若AC为⊙O的直径,PBC为⊙O的割线,E为弦AB的中点,PE的延长线交AC于E,且∠FPB=45°,点F到PC的距离为5,则FC的长为( )| A. | 10 | B. | 12 | C. | $5\sqrt{5}$ | D. | $5\sqrt{6}$ |
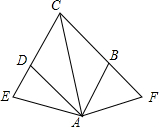 如图,点E.F分别是菱形ABCD的边CD与CB延长线上的点,且DE=BF,求证:∠E=∠F.
如图,点E.F分别是菱形ABCD的边CD与CB延长线上的点,且DE=BF,求证:∠E=∠F.
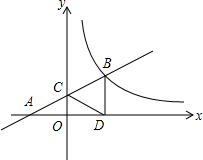 如图,在直角坐标系xOy中,直线y=mx+1经过点A(-2,0)与y轴正半轴交于C点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过B作BD⊥x轴于D,连接DC,若AC=CB.
如图,在直角坐标系xOy中,直线y=mx+1经过点A(-2,0)与y轴正半轴交于C点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点B,过B作BD⊥x轴于D,连接DC,若AC=CB. 如图,四边形ABCD是菱形,对角线AC与BD相交于点0,∠ACD=30°,BD=2.
如图,四边形ABCD是菱形,对角线AC与BD相交于点0,∠ACD=30°,BD=2.