题目内容
如图,在平面直角坐标系中,点A,B的坐标分别为A(0,α),B(b,α),且α、b满足(a-2)2+|b-4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
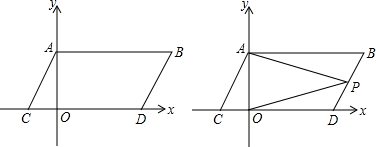
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合)
的值是否发生变化,并说明理由.

(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合)
| ∠BAP+∠DOP |
| ∠APO |
考点:坐标与图形性质,平行线的性质,三角形的面积,坐标与图形变化-平移
专题:
分析:(1)先由非负数性质求出a=2,b=4,再根据平移规律,得出点C,D的坐标,然后根据四边形ABDC的面积=AB×OA即可求解;
(2)存在.设M坐标为(0,m),根据S△PAB=S四边形ABDC,列出方程求出m的值,即可确定M点坐标;
(3)过P点作PE∥AB交OC与E点,根据平行线的性质得∠BAP+∠DOP=∠APE+∠OPE=∠APO,故比值为1.
(2)存在.设M坐标为(0,m),根据S△PAB=S四边形ABDC,列出方程求出m的值,即可确定M点坐标;
(3)过P点作PE∥AB交OC与E点,根据平行线的性质得∠BAP+∠DOP=∠APE+∠OPE=∠APO,故比值为1.
解答:解:(1)∵(a-2)2+|b-4|=0,
∴a=2,b=4,
∴A(0,2),B(4,2).
∵将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,
∴C(-1,0),D(3,0).
∴S四边形ABDC=AB×OA=4×2=8;
(2)在y轴上存在一点M,使S△MCD=S四边形ABCD.设M坐标为(0,m).
∵S△MCD=S四边形ABDC,
∴
×4|m|=8,
∴2|m|=8,
解得m=±4.
∴M(0,4)或(0,-4);
 (3)当点P在BD上移动时,
(3)当点P在BD上移动时,
=1不变,理由如下:
过点P作PE∥AB交OA于E.
∵CD由AB平移得到,则CD∥AB,
∴PE∥CD,
∴∠BAP=∠APE,∠DOP=∠OPE,
∴∠BAP+∠DOP=∠APE+∠OPE=∠APO,
∴
=1.
∴a=2,b=4,
∴A(0,2),B(4,2).
∵将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,
∴C(-1,0),D(3,0).
∴S四边形ABDC=AB×OA=4×2=8;
(2)在y轴上存在一点M,使S△MCD=S四边形ABCD.设M坐标为(0,m).
∵S△MCD=S四边形ABDC,
∴
| 1 |
| 2 |
∴2|m|=8,
解得m=±4.
∴M(0,4)或(0,-4);
 (3)当点P在BD上移动时,
(3)当点P在BD上移动时,| ∠BAP+∠DOP |
| ∠APO |
过点P作PE∥AB交OA于E.
∵CD由AB平移得到,则CD∥AB,
∴PE∥CD,
∴∠BAP=∠APE,∠DOP=∠OPE,
∴∠BAP+∠DOP=∠APE+∠OPE=∠APO,
∴
| ∠BAP+∠DOP |
| ∠APO |
点评:本题考查了坐标与图形平移的关系,坐标与平行四边形性质的关系,平行线的性质及三角形、平行四边形的面积公式.关键是理解平移规律,作平行线将相关角进行转化.

练习册系列答案
相关题目
 如图所示:三个村庄A、B、C之间的距离分别是AB=5km,BC=12km,AC=13km,要从B修一条公路BD直达AC,已知公路的造价2600万元/km,求修这条公路的最低造价是多少?
如图所示:三个村庄A、B、C之间的距离分别是AB=5km,BC=12km,AC=13km,要从B修一条公路BD直达AC,已知公路的造价2600万元/km,求修这条公路的最低造价是多少? 某电视塔AB和CD楼的水平距离为200m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高和楼高(
某电视塔AB和CD楼的水平距离为200m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高和楼高(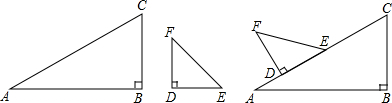
 如图,在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,同时,另一点Q由点B开始沿BC边向点C以1.5cm/s的速度运动.
如图,在Rt△ABC中,∠B=90°,AC=100cm,BC=80cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,同时,另一点Q由点B开始沿BC边向点C以1.5cm/s的速度运动.