题目内容
9. 如图所示,在三角形△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从A点出发沿AB以1cm/s的速度向B移动,点Q从B点出发沿BC以3cm/s的速度向C移动,如果P,Q分别从A,B同时出发,运动t秒后,△PBQ的面积等于s.
如图所示,在三角形△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从A点出发沿AB以1cm/s的速度向B移动,点Q从B点出发沿BC以3cm/s的速度向C移动,如果P,Q分别从A,B同时出发,运动t秒后,△PBQ的面积等于s.(1)求s与t之间的函数关系式,并写出自变量t的取值范围;
(2)求t为何值时,△PBQ的面积等于3;
(3)在(1)中,△PBQ的面积能否等于6cm2?说明理由.
分析 (1)分别表示出BP、BQ,继而可得s与t之间的函数关系式,根据AB、BC的长度及点P、Q的运动速度可得t的取值范围;
(2)当s=3时,解出t的值即可,注意判断t的取值是否在取值范围内;
(3)当s=6时,解出t的值即可,注意判断t的取值是否在取值范围内.
解答 解:(1)由题意得,BP=5-t(0≤t≤5),BQ=3t(0≤t≤$\frac{7}{3}$),
则s=$\frac{1}{2}$(5-t)×3t=-$\frac{3}{2}$t2+$\frac{15}{2}$(0≤t≤$\frac{7}{3}$).
(2)当s=3时,-$\frac{3}{2}$t2+$\frac{15}{2}$t=3,
整理化简得:t2-5t+2=0,
解得:t1=$\frac{5-\sqrt{17}}{2}$,t2=$\frac{5+\sqrt{17}}{2}$(舍去),
即当t=$\frac{5-\sqrt{17}}{2}$时,△PBQ的面积等于3;
(3)当s=6时,-$\frac{3}{2}$t2+$\frac{15}{2}$t=6,
整理化简得:t2-5t+4=0,
解得:t1=1,t2=4(舍去),
即当t=1时,△PBQ的面积等于6.
点评 本题考查了一元二次方程的应用及动点问题,解答本题的关键是表示出BP、BQ的长度,得出s与t的函数关系式,难度一般.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.为了解某市七年级学生的肺活量,从中随机抽样调查了400名学生的肺活量,这项调查中的样本是( )
| A. | 某市八年级学生的肺活量 | B. | 从中抽取的400名学生 | ||
| C. | 从中抽取的400名学生的肺活量 | D. | 400 |
17.一个角的余角是它的3倍,则这个角的度数是( )
| A. | 22.5° | B. | 25° | C. | 30° | D. | 20.5° |
4. 如图是根据长春市10月份某段时间的每天最低气温绘成的折线图,那么这段时间最低气温的极差、众数、平均数依次是( )
如图是根据长春市10月份某段时间的每天最低气温绘成的折线图,那么这段时间最低气温的极差、众数、平均数依次是( )
 如图是根据长春市10月份某段时间的每天最低气温绘成的折线图,那么这段时间最低气温的极差、众数、平均数依次是( )
如图是根据长春市10月份某段时间的每天最低气温绘成的折线图,那么这段时间最低气温的极差、众数、平均数依次是( )| A. | 5,5,4 | B. | 5,5,4.5 | C. | 2.8,5,4 | D. | 2.8,5,4.5 |
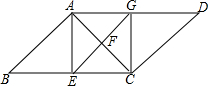 如图,在△ABC中,AB=AC,将△ABC绕点A逆时针方向旋转60°得到△ACD.
如图,在△ABC中,AB=AC,将△ABC绕点A逆时针方向旋转60°得到△ACD.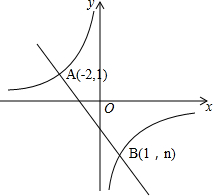 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于A、B两点,
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于A、B两点,