题目内容
14.若二次函数的图象的对称轴方程是x=$\frac{3}{2}$,并且图象过A(0,-4)和B(4,0)(1)求此二次函数图象上点A关于对称轴x=$\frac{3}{2}$对称的点A′的坐标;
(2)求此二次函数的解析式.
分析 (1)直接利用对称性求解即可;
(2)利用待定系数法把A(0,-4)和B(4,0),即对称轴x=$\frac{3}{2}$代入解析式,解三元一次方程组可得y=x2-3x-4.
解答 解:(1)A′(3,-4);
(2)设此二次函数的解析式为y=ax2+bx+c,
由题意,得$\left\{\begin{array}{l}{c=-4}\\{16a+4b+c=0}\\{-\frac{b}{2a}=\frac{3}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-3}\\{c=-4}\end{array}\right.$.
∴y=x2-3x-4.
点评 此题考查二次函数的性质,待定系数法求函数解析式,掌握二次函数的对称性是解决问题的关键.

练习册系列答案
相关题目
 如图中有6条线段,分别表示为AD,AC,AB,DC,DB,CB.
如图中有6条线段,分别表示为AD,AC,AB,DC,DB,CB.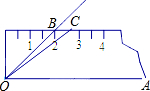 如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合.OB与尺上沿的交点B在尺上的读书恰为2厘米,若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数为2.7厘米.(结果精确到0.1厘米,参考数据sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,将45°的∠AOB按下面的方式放置在一把刻度尺上:顶点O与尺下沿的端点重合,OA与尺下沿重合.OB与尺上沿的交点B在尺上的读书恰为2厘米,若按相同的方式将37°的∠AOC放置在该刻度尺上,则OC与尺上沿的交点C在尺上的读数为2.7厘米.(结果精确到0.1厘米,参考数据sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 如图所示,在三角形△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从A点出发沿AB以1cm/s的速度向B移动,点Q从B点出发沿BC以3cm/s的速度向C移动,如果P,Q分别从A,B同时出发,运动t秒后,△PBQ的面积等于s.
如图所示,在三角形△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从A点出发沿AB以1cm/s的速度向B移动,点Q从B点出发沿BC以3cm/s的速度向C移动,如果P,Q分别从A,B同时出发,运动t秒后,△PBQ的面积等于s. 在△ABC中,∠BAC=90°,AD是BC边上的高,∠B=35°,则∠CAD=35°.
在△ABC中,∠BAC=90°,AD是BC边上的高,∠B=35°,则∠CAD=35°.