题目内容
18.(1)$\left\{\begin{array}{l}{x+2y=-2}\\{7x-4y=-41}\end{array}\right.$(2)$\left\{\begin{array}{l}{x+5=3(y-1)}\\{5(x-1)=3(y+5)}\end{array}\right.$
(3)$\left\{\begin{array}{l}{\frac{m+n}{3}+\frac{n-m}{4}=-\frac{1}{4}}\\{\frac{m+8}{6}-\frac{5(n+1)}{12}=2}\end{array}\right.$
(4)$\left\{\begin{array}{l}{83x+49y=98}\\{49x+83y=166}\end{array}\right.$.
分析 (1)方程组利用加减消元法求出解即可;
(2)方程组整理后,利用加减消元法求出解即可;
(3)方程组整理后,利用加减消元法求出解即可;
(4)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x+2y=-2①}\\{7x-4y=-41②}\end{array}\right.$,
①×2+②得:9x=-45,即x=-5,
把x=-5代入①得:y=$\frac{3}{2}$,
则方程组的解为$\left\{\begin{array}{l}{x=-5}\\{y=\frac{3}{2}}\end{array}\right.$;
(2)方程组整理得:$\left\{\begin{array}{l}{x-3y=-8①}\\{5x-3y=20②}\end{array}\right.$,
②-①得:4x=28,即x=7,
把x=7代入①得:y=5,
则方程组的解为$\left\{\begin{array}{l}{x=7}\\{y=5}\end{array}\right.$;
(3)方程组整理得:$\left\{\begin{array}{l}{m+7n=-3①}\\{2m-5n=13②}\end{array}\right.$,
①×2-②得:19n=-19,即n=-1,
把n=-1代入①得:m=4,
则方程组的解为$\left\{\begin{array}{l}{m=4}\\{n=-1}\end{array}\right.$;
(4)$\left\{\begin{array}{l}{83x+49y=98①}\\{49x+83y=166②}\end{array}\right.$,
①+②得:132(x+y)=264,即x+y=2③,
③×83-①得:34y=68,即y=2,
把y=2代入③得:x=0,
则方程组的解为$\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案| A. | AM=ME | B. | AM=BE | C. | AM=CN | D. | AM⊥MD |
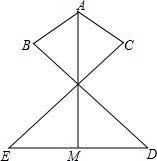 已知如图,AB=AC,∠BAM=∠CAM,CE=BD,M是ED的中点,试说明:AM⊥ED.
已知如图,AB=AC,∠BAM=∠CAM,CE=BD,M是ED的中点,试说明:AM⊥ED. 如图所示,在三角形△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从A点出发沿AB以1cm/s的速度向B移动,点Q从B点出发沿BC以3cm/s的速度向C移动,如果P,Q分别从A,B同时出发,运动t秒后,△PBQ的面积等于s.
如图所示,在三角形△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从A点出发沿AB以1cm/s的速度向B移动,点Q从B点出发沿BC以3cm/s的速度向C移动,如果P,Q分别从A,B同时出发,运动t秒后,△PBQ的面积等于s. 如图,在一幅矩形地毯的四周镶有宽度相同的花边,如图,地毯中央的矩形图案长8米、宽6米,整个地毯的面积是120平方米,求花边的宽.
如图,在一幅矩形地毯的四周镶有宽度相同的花边,如图,地毯中央的矩形图案长8米、宽6米,整个地毯的面积是120平方米,求花边的宽. 如图,已知DE∥BC,EF∥CD,且E在边AC上,F、D在边AB上,若AE:CE=2:1,DF=2,求AF、BD的长.
如图,已知DE∥BC,EF∥CD,且E在边AC上,F、D在边AB上,若AE:CE=2:1,DF=2,求AF、BD的长.