题目内容
11. 我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,
我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,(1)求山坡高度;
(2)为防夏季因瀑雨引发山体滑坡,保障安全,学校决定对山坡进行改造,经地质人员勘测,当坡角不超过45°时,可确保山体不滑坡,改造时保持坡脚A不动,从坡顶B 沿BC削进到E处,问BE至少是多少米(结果保留根号)?
分析 (1)作BG⊥AD于G.构建直角△ABG,通过解该直角三角形求得BG的长度,即山坡高度;
(2)作EF⊥AD于F.通过解直角△ABG得到线段AG的长度,然后解直角△AEF求得AF=EF=BG=20$\sqrt{3}$.所以BE=FG=AF-AG.
解答  解:(1)作BG⊥AD于G.
解:(1)作BG⊥AD于G.
∵Rt△ABG中,∠BAD=60°,AB=40,
∴BG=AB•sin60°=20$\sqrt{3}$,
∴山坡的高度为20$\sqrt{3}$米;
(2)作EF⊥AD于F.
AG=AB•cos60°=20.
同理在Rt△AEF中,∠EAD=45°,
∴AF=EF=BG=20$\sqrt{3}$,
∴BE=FG=AF-AG=20($\sqrt{3}$-1)米
∴BE至少20($\sqrt{3}$-1)米.
点评 主要考查解直角三角形的应用-坡度坡角问题.培养学生分析问题,综合利用解直角三角形的知识解决实际问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.下列命题中是真命题的是( )
| A. | 阴天会下雨是必然事件 | |
| B. | 若关于x的一元二次方程kx2-2x-1=0有实数根,则k≥-1 | |
| C. | 在平面直角坐标系中,如果位似是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k | |
| D. | 多边形的外角和等于360° |
6.若m与-3互为倒数,则m等于( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
3.顺次连接对角线互相垂直的四边形各边中点所得到的四边形是( )
| A. | 平行四边形 | B. | 正方形 | C. | 矩形 | D. | 菱形 |
20.已知直角坐标系中点P到y轴的距离为5,且点P到x轴的距离为3,则这样的点P的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
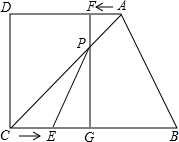 如图,在四边形ABCD中,AD∥BC,∠D=90°,BC=50,AD=36,CD=27.点E从C出发以每秒5个单位长度的速度向B运动,点F从A出发,以每秒4个单位长度的速度向D运动.两点同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.过点F作FG⊥BC,垂足为G,连结AC交FG于P,连结EP.
如图,在四边形ABCD中,AD∥BC,∠D=90°,BC=50,AD=36,CD=27.点E从C出发以每秒5个单位长度的速度向B运动,点F从A出发,以每秒4个单位长度的速度向D运动.两点同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.过点F作FG⊥BC,垂足为G,连结AC交FG于P,连结EP.