题目内容
3.顺次连接对角线互相垂直的四边形各边中点所得到的四边形是( )| A. | 平行四边形 | B. | 正方形 | C. | 矩形 | D. | 菱形 |
分析 根据三角形中位线的性质,可得到这个四边形是平行四边形,再由对角线垂直,能证出有一个角等于90°,则这个四边形为矩形.
解答 证明:如图,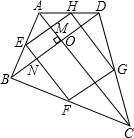 AC⊥BD,E、F、G、H分别为各边的中点,连接点E、F、G、H.
AC⊥BD,E、F、G、H分别为各边的中点,连接点E、F、G、H.
∵E、F、G、H分别为各边的中点,
∴EF∥AC,GH∥AC,EH∥BD,FG∥BD(三角形的中位线平行于第三边),
∴四边形EFGH是平行四边形(两组对边分别平行的四边形是平行四边形),
∵AC⊥BD,EF∥AC,EH∥BD,
∴∠EMO=∠ENO=90°,
∴四边形EMON是矩形(有三个角是直角的四边形是矩形),
∴∠MEN=90°,
∴四边形EFGH是矩形(有一个角是直角的平行四边形是矩形).
故选:C.
点评 本题考查了中点四边形.矩形的判定方法,常用的方法有三种:
①一个角是直角的平行四边形是矩形.
②三个角是直角的四边形是矩形.
③对角线相等的平行四边形是矩形.

练习册系列答案
相关题目
13.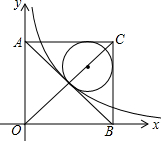 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(4-2$\sqrt{2}$)的圆内切于△ABC,则k的值为( )
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(4-2$\sqrt{2}$)的圆内切于△ABC,则k的值为( )
 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(4-2$\sqrt{2}$)的圆内切于△ABC,则k的值为( )
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(4-2$\sqrt{2}$)的圆内切于△ABC,则k的值为( )| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
18.某校九年级有19名同学参加跳绳比赛,预赛成绩各不相同,要取前9名参加决赛,小梅已经知道了自己的成绩,她想知道自己能否进入决赛,还需要知道这19名同学成绩的( )
| A. | 中位数 | B. | 众数 | C. | 平均数 | D. | 极差 |
8.已知$\sqrt{2x}$=2,则x等于( )
| A. | 4 | B. | ±2 | C. | 2 | D. | ±4 |
12.点(2,1)向上平移2个单位长度得到的点的坐标是( )
| A. | (2,0) | B. | (2,3) | C. | (4,1) | D. | (0,1) |
 我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,
我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,