题目内容
2.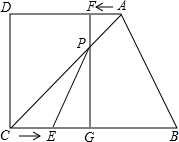 如图,在四边形ABCD中,AD∥BC,∠D=90°,BC=50,AD=36,CD=27.点E从C出发以每秒5个单位长度的速度向B运动,点F从A出发,以每秒4个单位长度的速度向D运动.两点同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.过点F作FG⊥BC,垂足为G,连结AC交FG于P,连结EP.
如图,在四边形ABCD中,AD∥BC,∠D=90°,BC=50,AD=36,CD=27.点E从C出发以每秒5个单位长度的速度向B运动,点F从A出发,以每秒4个单位长度的速度向D运动.两点同时出发,当其中一个动点到达终点时,另一个动点也随之停止运动.过点F作FG⊥BC,垂足为G,连结AC交FG于P,连结EP.(1)点E、F中,哪个点最先到达终点?
(2)求△PEC的面积S与运动时间t的函数表达式,并写出自变量t的取值范围.当t为何值时,S的值最大;
(3)当△CEP为锐角三角形时,求运动时间t的取值范围.
分析 (1)分别求得点E和点F到达终点的时间,进行比较即可;
(2)根据△APF∽△ACD,利用相似三角形的对应边的比相等,利用t表示出PF和PG的长,然后利用三角形的面积公式得到函数解析式;
(3)求得当∠CEP=90°时t的值,当∠CPE=90°时,由△GEP∽△GPS求得t的值,即可确定t的范围.
解答 解:(1)点E到达终点需要的时间是:$\frac{50}{5}$=10(秒),
点F到终点需$\frac{36}{4}$=9(秒),
则F最先到达终点;
(2)由题意得:AF=4t,CE=5t,
由△APF∽△ACD,
则$\frac{AF}{AD}$=$\frac{PF}{CD}$,得$\frac{4t}{36}$=$\frac{PF}{27}$,
∴PF=3t,PG=27-3t,
S=$\frac{1}{2}$CE•PG=$\frac{1}{2}$×5t•(27-3t)=-$\frac{15}{2}$t2+$\frac{135}{2}$t,自变量t的取值范围是:0≤t≤9,当t=4.5时,S的值最大;
(3)当∠CEP=90°时,5t+4t=36,解得:t=4,
当∠CPE=90°时,EG=9t-36,CG=36-4t,
由△GEP∽△GPS,得$\frac{GE}{PG}$=$\frac{PG}{CG}$,得方程(36t-4t)(9t-36)=(27-3t)2,
解得:t=5或9(舍去).
则运动时间t的取值范围是4<t<5.
点评 本题考查了相似三角形的判定与性质,利用相似三角形的性质,用t正确表示出PF和PG的值是本题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
13.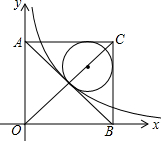 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(4-2$\sqrt{2}$)的圆内切于△ABC,则k的值为( )
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(4-2$\sqrt{2}$)的圆内切于△ABC,则k的值为( )
 如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(4-2$\sqrt{2}$)的圆内切于△ABC,则k的值为( )
如图,在平面直角坐标系中有一正方形AOBC,反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点,半径为(4-2$\sqrt{2}$)的圆内切于△ABC,则k的值为( )| A. | 4$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{2}$ | D. | 2 |
10.刻画一组数据波动大小的统计量是( )
| A. | 平均数 | B. | 方差 | C. | 众数 | D. | 中位数 |
12.点(2,1)向上平移2个单位长度得到的点的坐标是( )
| A. | (2,0) | B. | (2,3) | C. | (4,1) | D. | (0,1) |
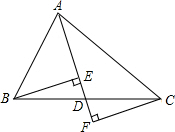 如图,在△ABC中,点D是BC边的中点,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:DE=DF.
如图,在△ABC中,点D是BC边的中点,分别过点B、C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F,求证:DE=DF.
 我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,
我市某乡镇学校教学楼后面靠近一座山坡,坡面上是一块平地,如图所示,BC∥AD,斜坡AB=40米,坡角∠BAD=60°,