题目内容
17.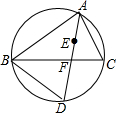 如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D,连接BD,且AB=AD,则∠ABC的度数为( )
如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D,连接BD,且AB=AD,则∠ABC的度数为( )| A. | $\frac{3}{2}$∠D-90° | B. | 90°-$\frac{1}{2}$∠D | C. | 180°-∠D | D. | 3∠D-180° |
分析 由内心的性质和圆周角定理可证得∠BAD=∠CBD由等腰三角形的性质得到∠ABD=∠D,即∠BAD=∠CBD=180°-2∠D,再由三角形内角和定理化简即可推得结论.
解答 解∵E是△ABC的内心,
∴∠BAD=∠CAD,
∵∠CAD=∠CBD,
∴∠BAD=∠CBD,
设∠BAD=∠CBD=x,
∵AB=AD,
∴∠ABD=∠D,
∴x=180°-2∠D,
在△ABD中,∠BAD+∠ABD+∠D=180°,
即∠ABC+x+x+∠D=180°,
∴∠ABC+2(180°-2∠D)+∠D=180°,
∴∠ABC=3∠D-180°,
故选D.
点评 本题主要考查三角形的内心,等腰三角形的性质,三角形内角和,掌握三角形的内心即三角形三条内角平分线的交点是解题的关键.

练习册系列答案
相关题目
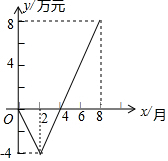 某超市今年年初因管理不善,效益较差,连续几个月出现亏损,后改革管理方法,实行股份制,员工积极性大增,业绩逐步上升,1-8月的累计利润y(万元)与时间x(月)之间的关系如图,根据图象回答:
某超市今年年初因管理不善,效益较差,连续几个月出现亏损,后改革管理方法,实行股份制,员工积极性大增,业绩逐步上升,1-8月的累计利润y(万元)与时间x(月)之间的关系如图,根据图象回答:
 如图,在直角三角尺ABC中,∠C=90°,把直角三角尺ABC放置在圆上,AB经过圆心O,AC与⊙O相交于D,E两点,点C,D,E的刻度分别是0cm,2cm,5cm,BC与⊙O相切于F点,那么⊙O的半径是3.5cm.
如图,在直角三角尺ABC中,∠C=90°,把直角三角尺ABC放置在圆上,AB经过圆心O,AC与⊙O相交于D,E两点,点C,D,E的刻度分别是0cm,2cm,5cm,BC与⊙O相切于F点,那么⊙O的半径是3.5cm.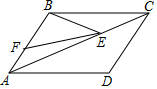 已知,如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E为AD上,BE=12cm,CE=5cm,则?ABCD的周长为39cm.
已知,如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E为AD上,BE=12cm,CE=5cm,则?ABCD的周长为39cm.
 如图,在菱形ABCD中,tanA=$\sqrt{3}$,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=$\frac{\sqrt{3}}{4}$CG2;其中正确结论的序号为(1)(3)(4).
如图,在菱形ABCD中,tanA=$\sqrt{3}$,点E、F分别是AB、AD上任意的点(不与端点重合),且AE=DF,连接BF与DE相交于点G,连接CG与BD相交于点H,给出如下几个结论:(1)△AED≌△DFB;(2)CG与BD一定不垂直;(3)∠BGE的大小为定值;(4)S四边形BCDG=$\frac{\sqrt{3}}{4}$CG2;其中正确结论的序号为(1)(3)(4).