题目内容
6.阅读材料:如图1,在平面直角坐标系中,A、B两点的坐标分别为A(x1,y1),B(x2,y2),AB中点P的坐标为(xp,yp).由xp-x1=x2-xp,得xp=$\frac{{x}_{1}+{x}_{2}}{2}$,同理yp=$\frac{{y}_{1}+{y}_{2}}{2}$,所以AB的中点坐标为($\frac{{x}_{1}+{x}_{2}}{2}$,$\frac{{y}_{1}+{y}_{2}}{2}$).由勾股定理得AB2=|x2-x1|2+|y2-y1|2,所以A、B两点间的距离公式为AB=$\sqrt{({x}_{2}-{x}_{1})^{2}+({y}_{2}-{y}_{1})^{2}}$.这两公式对A、B在平面直角坐标系中其它位置也成立.解答下列问题: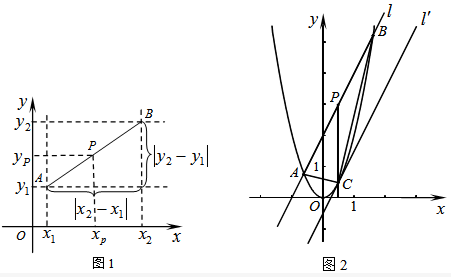
(1)已知M(1,-2),N(-1,2),直接利用公式填空:MN中点坐标为(0,0),MN=2$\sqrt{5}$.
如图2,直线l:y=2x+2与抛物线y=2x2交于A、B两点,P为AB的中点,过P作x轴的垂线交抛物线于点C.
(a)求A、B两点的坐标及C点的坐标;
(b)连结AB、AC,求证△ABC为直角三角形;
(c)将直线l平移到C点时得到直线l′,求两直线l与l′的距离.
分析 (1)根据中点坐标公式,两点间的距离公式,可得答案;
(a)根据解方程组,可得A,B点坐标,根据中点坐标公式,可得P点坐标,根据平行于y轴的直线横坐标相等,可得C点横坐标,根据自变量与函数值的对应关系,可得C点坐标;
(b)根据勾股定理及勾股定理的逆定理,可得答案;
(c)根据三角形的面积不同表示,可得关于CD的方程,根据解方程,可得答案.
解答 解:(1)由中点坐标,得$\frac{1+(-1)}{2}$=0,$\frac{2+(-2)}{2}$=0,
MN中点坐标为(0,0),
由两点间的距离,得
MN=$\sqrt{(1+1)^{2}+(-2-2)^{2}}$=2$\sqrt{5}$,
故答案为:(0,0),2$\sqrt{5}$.
(a)联立直线、抛物线,得$\left\{\begin{array}{l}{y=2x+2}\\{y=2{x}^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{1+\sqrt{5}}{2}}\\{y=3+\sqrt{5}}\end{array}\right.$,$\left\{\begin{array}{l}{x=\frac{1-\sqrt{5}}{2}}\\{y=3-\sqrt{5}}\end{array}\right.$,
即B($\frac{1+\sqrt{5}}{2}$,3+$\sqrt{5}$),A($\frac{1-\sqrt{5}}{2}$,3-$\sqrt{5}$).
由P是AB的中点,得
P($\frac{1}{2}$,3)
当x=$\frac{1}{2}$时,y=2x2=$\frac{1}{2}$,即C点坐标为($\frac{1}{2}$,$\frac{1}{2}$).
(b)AB2=($\frac{1+\sqrt{5}}{2}$-$\frac{1-\sqrt{5}}{2}$)2+(3+$\sqrt{5}$-3+$\sqrt{5}$)2=25;
BC2=($\frac{1+\sqrt{5}}{2}$-$\frac{1}{2}$)2+(3+$\sqrt{5}$-$\frac{1}{2}$)2=$\frac{25}{2}$-5$\sqrt{5}$;
AC2=($\frac{1-\sqrt{5}}{2}$-$\frac{1}{2}$)2+(3-$\sqrt{5}$-$\frac{1}{2}$)2=$\frac{25}{2}$+5$\sqrt{5}$,
∵AC2+BC2=AB2,
∴∠ACB=90°
∴△ABC是直角三角形;
(c)如图 ,
,
作CD⊥AB于D点,CD 是两直线间的距离,
S△ABC=$\frac{1}{2}$AB•CD=$\frac{1}{2}$AC•BC,
$\frac{1}{2}$×5CD=$\frac{1}{2}$$\sqrt{\frac{25}{2}+5\sqrt{5}}$×$\sqrt{\frac{25}{2}-5\sqrt{5}}$,
解得CD=$\frac{\sqrt{5}}{2}$.
两直线l与l′的距离是$\frac{\sqrt{5}}{2}$.
点评 本题考查了二次函数综合题,解(1)的关键是利用中点坐标公式,两点间的距离公式;解a的关键是利用中点坐标公式得出P点坐标,又利用了平行于y轴的直线横坐标相等,自变量与函数值的对应关系;解b的关键是利用勾股定理及勾股定理的逆定理,解c的关键是利用面积的不同表示法.

| 方式一 | 方式二 | |
| 月租费/(元/月) | 30 | 0 |
| 本地通话费/(元/min) | 0.30 | 0.40 |
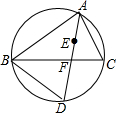 如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D,连接BD,且AB=AD,则∠ABC的度数为( )
如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D,连接BD,且AB=AD,则∠ABC的度数为( )| A. | $\frac{3}{2}$∠D-90° | B. | 90°-$\frac{1}{2}$∠D | C. | 180°-∠D | D. | 3∠D-180° |
| A. | 1+(-2) | B. | 1-(-2) | C. | 1×(-2) | D. | 1÷(-2) |
 在平行四边形ABCD中,点O是对角线AC、BD的交点,AC⊥BC,且AB=10cm,AD=6cm,则AO=4cm.
在平行四边形ABCD中,点O是对角线AC、BD的交点,AC⊥BC,且AB=10cm,AD=6cm,则AO=4cm. 如图,一次函数y=ax+b的图象与x轴交于点A,与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点B(-2,n),过点B作BC⊥x轴于点C,点P(-4-n,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,分别求反比例函数和一次函数的解析式.
如图,一次函数y=ax+b的图象与x轴交于点A,与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点B(-2,n),过点B作BC⊥x轴于点C,点P(-4-n,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,分别求反比例函数和一次函数的解析式. 如图,在菱形ABCD中,∠BAD=120°,BC=1,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为$\sqrt{3}$-1.
如图,在菱形ABCD中,∠BAD=120°,BC=1,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为$\sqrt{3}$-1. 如图,矩形ABCD中,AB=4,BC=6,点E为BC的中点,连接AE,将△ABE沿AE折叠,点B落在点B′处,则sin∠B′EC的值为$\frac{24}{25}$.
如图,矩形ABCD中,AB=4,BC=6,点E为BC的中点,连接AE,将△ABE沿AE折叠,点B落在点B′处,则sin∠B′EC的值为$\frac{24}{25}$.