题目内容
9.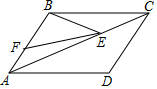 已知,如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E为AD上,BE=12cm,CE=5cm,则?ABCD的周长为39cm.
已知,如图,在?ABCD中,BE、CE分别平分∠ABC、∠BCD,E为AD上,BE=12cm,CE=5cm,则?ABCD的周长为39cm.
分析 根据角平分线的定义和平行线的性质得到等腰三角形ABE和等腰三角形CDE和直角三角形BCE.根据直角三角形的勾股定理得到BC=13.根据等腰三角形的性质得到AB=CD=$\frac{1}{2}$AD=$\frac{1}{2}$BC=6.5cm,从而求得该平行四边形的周长.
解答 解:如图所示:在平行四边形ABCD中,
∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABE=∠EBC,∠BCE=∠ECD.,
∴∠EBC+∠BCE=90°,
∴∠BEC=90°,
∴BC2=BE2+CE2=122+52=132
∴BC=13cm,
∵AD∥BC,
∴∠AEB=∠EBC,
∴∠AEB=∠ABE,
∴AB=AE,
同理CD=ED,
∵AB=CD,
∴AB=AE=CD=ED=$\frac{1}{2}$BC=6.5cm,
∴平行四边形ABCD的周长=2(AB+BC)=2(6.5+13)=39cm;
故答案为:39cm.
点评 本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
17.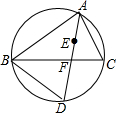 如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D,连接BD,且AB=AD,则∠ABC的度数为( )
如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D,连接BD,且AB=AD,则∠ABC的度数为( )
 如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D,连接BD,且AB=AD,则∠ABC的度数为( )
如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D,连接BD,且AB=AD,则∠ABC的度数为( )| A. | $\frac{3}{2}$∠D-90° | B. | 90°-$\frac{1}{2}$∠D | C. | 180°-∠D | D. | 3∠D-180° |
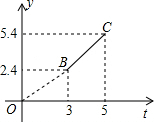 图中折线OBC表示从甲地向乙地打长途电话所付的电话费y(元)与通话时间x(分钟)之间的关系图象.
图中折线OBC表示从甲地向乙地打长途电话所付的电话费y(元)与通话时间x(分钟)之间的关系图象.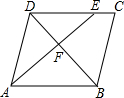 如图所示,在?ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为9:16.
如图所示,在?ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为9:16.
 在平行四边形ABCD中,点O是对角线AC、BD的交点,AC⊥BC,且AB=10cm,AD=6cm,则AO=4cm.
在平行四边形ABCD中,点O是对角线AC、BD的交点,AC⊥BC,且AB=10cm,AD=6cm,则AO=4cm. 如图,在菱形ABCD中,∠BAD=120°,BC=1,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为$\sqrt{3}$-1.
如图,在菱形ABCD中,∠BAD=120°,BC=1,点P是这个菱形内部或边上的一点,若以点P、B、C为顶点的三角形是等腰三角形,则P、D(P、D两点不重合)两点间的最短距离为$\sqrt{3}$-1. 如图,数轴上的点A、B、C、D、E表示连接的五个整数,若点A、E表示的数分别为x、y,且x+y=2,则点C表示的数为( )
如图,数轴上的点A、B、C、D、E表示连接的五个整数,若点A、E表示的数分别为x、y,且x+y=2,则点C表示的数为( )