Question

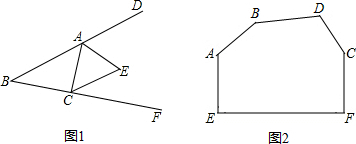
8．（1）如图1，在△ABC中，∠B=47°，三角形的外角∠DAC和∠ACF的平分线交于点E，求∠AEC的度数．
（2）如图2，六边形AEFCDB是一块模板，按规定，AB，CD的延长线相交应成85°角，已知，∠A+∠E+∠F+∠C=455°，请问：AB，CD的延长线相交所成的角是否符合规定，请说明理由．

Answer 1

分析 （1）根据三角形内角和定理、角平分线的定义以及三角形外角定理求得$\frac{1}{2}$∠DAC+$\frac{1}{2}$∠ACF=$\frac{1}{2}$（∠B+∠B+∠1+∠2）；最后在△AEC中利用三角形内角和定理可以求得∠AEC的度数．
（2）利用三角形外角性质得到：∠B+∠D=720°-455°=265°，则∴∠B+∠D=720°-455°=265°．

解答 解：（1）∵∠B=47°，
∴∠BAC+∠BCA=180°-47°=133°，
∴∠CAD+∠ACF=360°-133°=227°．
又∵AE和CE是角平分线，
∴∠CAE+∠ACE=113.5°，
∴∠E=180°-113.5°=66.5°；

（2）符合规定；                                               
证明：∵∠A+∠E+∠F+∠C=455°，
∴∠B+∠D=720°-455°=265°，
∴AB，CD的延长线相交成85°的角．

点评 本题考查了三角形内角和定理、三角形外角性质．解题时注意挖掘出隐含在题干中已知条件“三角形内角和是180°”．