题目内容
若a-b=2，a-c=1，则（2a-b-c）2+（c-b）2的值为（ ）
| A、10 | B、11 | C、9 | D、12 |
考点：代数式求值
专题：计算题
分析：由已知等式求出2a-b-c与c-b的值，代入原式计算即可得到结果．
解答：解：由a-b=2，a-c=1，得到2a-b-c=3，c-b=1，
则原式=9+1=10，
故选A
则原式=9+1=10，
故选A
点评：此题考查了代数式求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
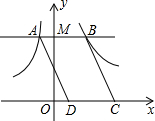如图，过y轴上一个动点M作x轴的平行线，交双曲线y=-| 4 |
| x |
| 10 |
| x |
| A、7 | B、10 | C、14 | D、28 |
平面直角坐标系内一点P（-3，2）关于原点对称的点的坐标是（ ）
| A、（2，-3） |
| B、（3，-2） |
| C、（-2，-3） |
| D、（2，3） |
下列计算正确的是（ ）
| A、2a+b=2ab |
| B、3x2-x2=2 |
| C、7mn-7nm=0 |
| D、a+a=a2 |
下列化简，正确的是（ ）
| A、-[-（-10）]=-10 |
| B、-（-3）=-3 |
| C、-（+5）=5 |
| D、-[-（+8）]=-8 |
若抛物线y=x2-2x+c与y轴的交点为（0，-3），则下列说法不正确的是（ ）
| A、抛物线开口向上 |
| B、抛物线与x轴的交点为（-1，0），（3，0） |
| C、当x=1时，y的最大值为-4 |
| D、抛物线的对称轴是直线x=1 |
