题目内容
 如图,△OAB绕点O逆时针旋转85°到△OCD的位置,已知∠A=80°,∠D=60°则∠AOD等于( )
如图,△OAB绕点O逆时针旋转85°到△OCD的位置,已知∠A=80°,∠D=60°则∠AOD等于( )| A、55° | B、45° |
| C、40° | D、35° |
考点:旋转的性质
专题:计算题
分析:先根据旋转的性质得∠BOD=85°,∠D=∠B=60°,再根据三角形内角和定理计算出∠AOB=180°-∠A-∠B=40°,然后利用∠AOD=∠BOD-∠AOB进行计算即可.
解答:解:∵△OAB绕点O逆时针旋转85°到△OCD的位置,
∴∠BOD=85°,∠D=∠B=60°,
∵∠A=80°,∠B=60°,
∴∠AOB=180°-∠A-∠B=40°,
∴∠AOD=∠BOD-∠AOB=85°-40°=45°.
故选B.
∴∠BOD=85°,∠D=∠B=60°,
∵∠A=80°,∠B=60°,
∴∠AOB=180°-∠A-∠B=40°,
∴∠AOD=∠BOD-∠AOB=85°-40°=45°.
故选B.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
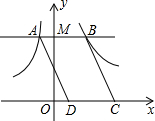 如图,过y轴上一个动点M作x轴的平行线,交双曲线y=-
如图,过y轴上一个动点M作x轴的平行线,交双曲线y=-| 4 |
| x |
| 10 |
| x |
| A、7 | B、10 | C、14 | D、28 |
下列计算正确的是( )
| A、2a+b=2ab |
| B、3x2-x2=2 |
| C、7mn-7nm=0 |
| D、a+a=a2 |
下列化简,正确的是( )
| A、-[-(-10)]=-10 |
| B、-(-3)=-3 |
| C、-(+5)=5 |
| D、-[-(+8)]=-8 |
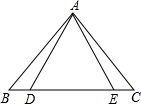 如图,△ABE≌△ACD,AB=AC,BE=CD,∠B=60°,∠AEC=120°,则∠DAC的度数等于( )
如图,△ABE≌△ACD,AB=AC,BE=CD,∠B=60°,∠AEC=120°,则∠DAC的度数等于( )| A、120° | B、70° |
| C、60° | D、50° |
若抛物线y=x2-2x+c与y轴的交点为(0,-3),则下列说法不正确的是( )
| A、抛物线开口向上 |
| B、抛物线与x轴的交点为(-1,0),(3,0) |
| C、当x=1时,y的最大值为-4 |
| D、抛物线的对称轴是直线x=1 |
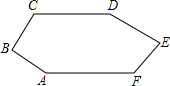 如图,已知CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=124°,∠E=80°,求∠F的大小.
如图,已知CD∥AF,∠CDE=∠BAF,AB⊥BC,∠C=124°,∠E=80°,求∠F的大小.