题目内容
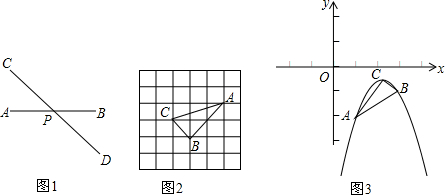
17.如果有两点到一条直线的距离相等,那么称这条直线为“两点的等距线”.(1)如图1,直线CD经过线段AB的中点P,试说明直线CD是点A、B的一条等距线.
(2)如图2,A、B、C是正方形网格中的三个格点,请在网格中作出所有的直线m,使直线m过点C且直线m是“A、B的等距线”.
(3)如图3,抛物线y=-x2+bx+c过点A(1,-2),B(3,-1),顶点为C.抛物线上是否存在点P,使S△APC=SBPC?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)分别作AE⊥CD,BF⊥CD,垂足为E,F,利用AAS证明△AEP≌△AFP,得到AE=BF即可证明直线CD是点A、B的一条等距线;
(2)根据两点等距线的定义直接作出图形;
(3)首先利用待定系数法求出二次函数的解析式,然后由S△APC=SBPC可得A、B两点到直线PC的距离相等,再分两类进行讨论,即可求出点P的坐标.
解答  (1)证明:分别作AE⊥CD,BF⊥CD,垂足为E,F,
(1)证明:分别作AE⊥CD,BF⊥CD,垂足为E,F,
∴∠AEP=∠BFP=90°,
∵P是AB中点,
∴AP=BP,
在△AEP和△AFP,
$\left\{\begin{array}{l}{∠AEP=∠BFP=90°}\\{∠APE=∠BPF}\\{AP=BP}\end{array}\right.$,
∴△AEP≌△AFP(AAS)
∴AE=BF,即直线CD是点A、B的一条等距线.
(2)如图2 ,直线m1、m2就是所有的直线;
,直线m1、m2就是所有的直线;
(3)由题意可知$\left\{\begin{array}{l}{-1+b+c=-2}\\{-9+3b+c=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=\frac{9}{2}}\\{c=-\frac{11}{2}}\end{array}\right.$,
∴抛物线为y=-x2+$\frac{9}{2}$x-$\frac{11}{2}$,
∵S△APC=S△BPC,
∴A、B两点到直线PC的距离相等,
①当PC∥AB时,计算得直线AB解析式为y=$\frac{1}{2}$x-$\frac{5}{2}$,直线CP解析式为y=$\frac{1}{2}$x-$\frac{25}{16}$,
联立$\left\{\begin{array}{l}{y=-{x}^{2}+\frac{9}{2}x-\frac{11}{2}}\\{y=\frac{1}{2}x-\frac{25}{16}}\end{array}\right.$
解得x1=$\frac{7}{4}$,x2=$\frac{9}{4}$;
∴点P($\frac{7}{4}$,-$\frac{11}{16}$),
②当直线CP过AB中点时,易求AB中点E(2,-$\frac{3}{2}$),直线CE解析式为y=$\frac{17}{4}$x-10,
联立$\left\{\begin{array}{l}{y=-{x}^{2}+\frac{9}{2}x-\frac{11}{2}}\\{y=\frac{17}{4}x-10}\end{array}\right.$,
解得x1=-2,x2=$\frac{9}{4}$;
∴点P(-2,-$\frac{37}{2}$),
综上所述,存在点P($\frac{7}{4}$,-$\frac{11}{16}$) 或(-2,-$\frac{37}{2}$) 使S△APC=SBPC.
点评 本题主要考查了二次函数综合题的知识,此题涉及到点到直线的距离、待定系数法求二次函数解析式、一次函数解析式以及抛物线与直线的交点等知识,解答本题的关键是理解两点间的等距线的定义,此题有一定的难度.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案| A. | 等腰三角形 | B. | 平行四边形 | C. | 矩形 | D. | 菱形 |
| A. | 2.51×10-6米 | B. | 2.51×10-5米 | C. | 2.51×10-4米 | D. | 2.51×10-3米 |
| A. | S | B. | π | C. | r | D. | S和r |
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 无法判断 |
| A. | 无实根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 不确定 |
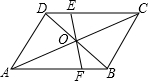 如图,?ABCD中,EF过对角线的交点O分别与CD、AB交于点E、F,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )
如图,?ABCD中,EF过对角线的交点O分别与CD、AB交于点E、F,AB=4,AD=3,OF=1.3,则四边形BCEF的周长为( )| A. | 8.3 | B. | 9.6 | C. | 12.6 | D. | 13.6 |
| A. | 正数 | B. | 零 | C. | 负数 | D. | 非负数 |