题目内容
7.不论x、y为何有理数时,x2+y2-12x+4y+40的值均为( )| A. | 正数 | B. | 零 | C. | 负数 | D. | 非负数 |
分析 将式子配方,再判断式子的取值范围即可.
解答 解:∵x2+y2-12x+4y+40=(x-6)2+(y-2)2≥0,
∴多项式x2+y2-12x+4y+40的值都是非负数.
故选:D.
点评 本题考查了配方法,非负数的运用.关键是将多项式分组,写成非负数的和的形式.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
16.在多项式x2+9中添加一个单项式,使其成为一个完全平方式,则添加的单项式可以是( )
| A. | x | B. | 3x | C. | 6x | D. | 9x |
17.检查4个篮球的质量,把超过标准质量的克数记为正数,不足标准质量的克数记为负数,检查的结果如表:则质量较好的篮球的编号是( )
| 篮球的编号 | 1 | 2 | 3 | 4 |
| 与标准质量的差(克) | +4 | +5 | -5 | -3 |
| A. | 1号 | B. | 2号 | C. | 3号 | D. | 4号 |
 已知,如图,△ABC中,DE∥FG∥BC,AD:DF:FB=1:2:3,若EG=3,则AC=9.
已知,如图,△ABC中,DE∥FG∥BC,AD:DF:FB=1:2:3,若EG=3,则AC=9. 下面的图象反映的是小明从家跑步去图书馆,在那里锻炼了一阵后又走到文具店去买本,然后散步回家.图中x表示时间,y表示小明离家的距离.
下面的图象反映的是小明从家跑步去图书馆,在那里锻炼了一阵后又走到文具店去买本,然后散步回家.图中x表示时间,y表示小明离家的距离. 如图,点O是直线l上一点,点A、B位于直线l的两侧,且∠AOB=90°,OA=OB,分别过A、B两点作AC⊥l,交直线l于点C,BD⊥l,交直线l于点D.求证:AC=OD.
如图,点O是直线l上一点,点A、B位于直线l的两侧,且∠AOB=90°,OA=OB,分别过A、B两点作AC⊥l,交直线l于点C,BD⊥l,交直线l于点D.求证:AC=OD.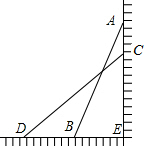 如图,将长为2.5米长的梯子AB斜靠在墙上,BE长0.7米.
如图,将长为2.5米长的梯子AB斜靠在墙上,BE长0.7米.