题目内容
9.解方程(1)3x(x-2)=2(2-x)
(2)x2-$\sqrt{2}$x-1=0
(3)$\frac{1{-x}^{2}}{2}$+$\frac{2-x}{3}$=$\frac{1}{3}$.
分析 (1)把方程化成一元二次方程的一般形式,然后方程左边的多项式利用平方差公式分解因式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解.
(2)找出a,b及c的值,计算出根的判别式的值大于0,代入求根公式即可求出解;
(3)方程去分母化简以后,方程左边的多项式利用平方差公式分解因式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程,求出一次方程的解即可得到原方程的解.
解答 解:(1)3x(x-2)=2(2-x)
(3x+2)(x-2)=0,
3x+2=0或x-2=0,
∴x1=-$\frac{2}{3}$,x2=2;
(2)x2-$\sqrt{2}$x-1=0,
∵a=1,b=-$\sqrt{2}$,c=-1,
∴b2-4ac=6>0,
∴x=$\frac{\sqrt{2}±\sqrt{6}}{2×1}$
∴x1=$\frac{\sqrt{2}+\sqrt{6}}{2}$,x2=$\frac{\sqrt{2}-\sqrt{6}}{2}$;
(3)$\frac{1{-x}^{2}}{2}$+$\frac{2-x}{3}$=$\frac{1}{3}$,
原方程化为:3x2+2x-5=0,
(3x+5)(x-1)=0,
3x+5=0或x-1=0,
∴x1=-$\frac{5}{3}$,x2=1.
点评 此题考查了解一元二次方程-因式分解法、公式法,利用因式分解法解方程时,首先将方程右边化为0,左边化为积的形式,然后利用两数相乘积为0,两因式中至少有一个为0转化为两个一元一次方程来求解.

练习册系列答案
相关题目
20.在同一个平面内的两条直线的位置关系有( )
| A. | 平行或垂直 | B. | 垂直或相交 | C. | 平行或相交 | D. | 平行、垂直或相交 |
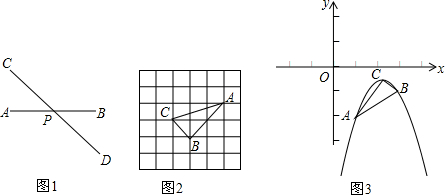
 如图,矩形ABCD对角线AC=10,BC=6,则图中四个小矩形的周长和为28.
如图,矩形ABCD对角线AC=10,BC=6,则图中四个小矩形的周长和为28.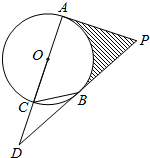 如图,已知PA、PB是⊙O的切线,A、B为切点.直径AC的延长线与PB的延长线交于点D.
如图,已知PA、PB是⊙O的切线,A、B为切点.直径AC的延长线与PB的延长线交于点D. 为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出17个这样的停车位($\sqrt{2}$≈1.4)
为解决停车难的问题,在如图一段长56米的路段开辟停车位,每个车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出17个这样的停车位($\sqrt{2}$≈1.4) 已知,如图,△ABC中,DE∥FG∥BC,AD:DF:FB=1:2:3,若EG=3,则AC=9.
已知,如图,△ABC中,DE∥FG∥BC,AD:DF:FB=1:2:3,若EG=3,则AC=9.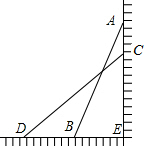 如图,将长为2.5米长的梯子AB斜靠在墙上,BE长0.7米.
如图,将长为2.5米长的梯子AB斜靠在墙上,BE长0.7米.