题目内容
17.不等式组$\left\{\begin{array}{l}{x≤3}\\{x>-1}\end{array}\right.$的解集为-1<x≤3,这个不等式组的整数解是0、1、2、3.分析 根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集,在该解集内确定整数解即可.
解答 解:不等式组$\left\{\begin{array}{l}{x≤3}\\{x>-1}\end{array}\right.$的解集为:-1<x≤3,
符合该不等式组的整数解为:0,1,2,3;
故答案为:-1<x≤3;0、1、2、3.
点评 本题考查的是一元一次不等式组的整数解,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
7.某自行车厂计划平均每天生产200辆,但是由于种种原因,实际每天生产量与计划量相比有出入.表是某周的生产情况(超产记为正,减产记为负):
(1)根据记录的数据可知该厂星期三生产自行车多少辆?
(2)产量最多的一天比产量最少的一天多生产自行车多少辆?
(3)根据记录的数据可知该厂本周实际共生产自行车多少辆?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +6 | -3 | -7 | +14 | -10 | +16 | -4 |
(2)产量最多的一天比产量最少的一天多生产自行车多少辆?
(3)根据记录的数据可知该厂本周实际共生产自行车多少辆?
8.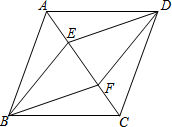 如图,在四边形ABCD中,AB∥CD,点E、F在对角线AC上,且∠ABF=∠CDE,
如图,在四边形ABCD中,AB∥CD,点E、F在对角线AC上,且∠ABF=∠CDE,
AE=CF.
(1)求证:△ABF≌△CDE;
(2)当四边形ABCD满足什么条件时,四边形BFDE是菱形?为什么?
 如图,在四边形ABCD中,AB∥CD,点E、F在对角线AC上,且∠ABF=∠CDE,
如图,在四边形ABCD中,AB∥CD,点E、F在对角线AC上,且∠ABF=∠CDE,AE=CF.
(1)求证:△ABF≌△CDE;
(2)当四边形ABCD满足什么条件时,四边形BFDE是菱形?为什么?
12.“PM2.5”是指大气中危害健康的直径小于2.5微米的颗粒物,也称可入肺颗粒物.公众对于大气环境质量越来越关注,某市为了了解市民对于“PM 2.5浓度升高时,对于户外活动的影响”的态度,随机抽取了部分市民进行调查.根据调查的相关数据,绘制的统计图表如下:
根据以上信息解答下列问题:
(1)直接写出统计表中M的值;
(2)根据以上信息,请补全条形统计图;
(3)如果该市约有市民400万人,根据上述信息,请你估计一下持有“影响很大,尽可能不去户外活动”这种态度的约有多少万人.
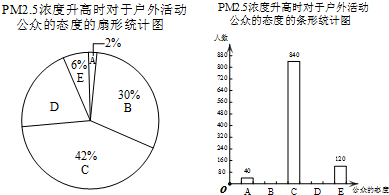
| PM2.5浓度升高时,对于户外活动是否有影响,您的态度是 | 百分比 |
| A.没有影响 | 2% |
| B.影响不大,还可以进行户外活动 | 30% |
| C.有影响,减少户外活动 | 42% |
| D.影响很大,尽可能不去户外活动 | m |
| E.不关心这个问题 | 6% |
(1)直接写出统计表中M的值;
(2)根据以上信息,请补全条形统计图;
(3)如果该市约有市民400万人,根据上述信息,请你估计一下持有“影响很大,尽可能不去户外活动”这种态度的约有多少万人.

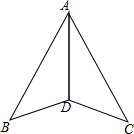 如图,∠ADB=∠ADC,AD平分∠BAC,你能证明△ABD≌△ACD吗?若BD=3cm,则CD有多长?
如图,∠ADB=∠ADC,AD平分∠BAC,你能证明△ABD≌△ACD吗?若BD=3cm,则CD有多长?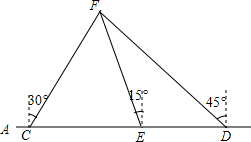 如图,在东西方向的海岸线AB上,有C、D两艘巡逻船,现均收到故障船F的求救信号,已知C、D两船相距50($\sqrt{2}$+$\sqrt{6}$)海里,船F在船C的北偏东30°方向上,船F在船D的西北方向上,海岸线AB上有一观测点E,测得船F正好在观测点E的北偏西15°方向上.
如图,在东西方向的海岸线AB上,有C、D两艘巡逻船,现均收到故障船F的求救信号,已知C、D两船相距50($\sqrt{2}$+$\sqrt{6}$)海里,船F在船C的北偏东30°方向上,船F在船D的西北方向上,海岸线AB上有一观测点E,测得船F正好在观测点E的北偏西15°方向上.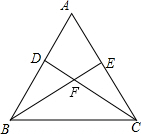 在△ABC中,AB=AC,D,E分别在边AB,AC上,AD=AE,DC,BE交于点F,求证:△BDC≌△CEB.
在△ABC中,AB=AC,D,E分别在边AB,AC上,AD=AE,DC,BE交于点F,求证:△BDC≌△CEB.