题目内容
20.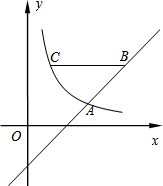 如图,在直角坐标系xOy中,反比例函数图象与直线y=x-2相交于横坐标为3的点A.
如图,在直角坐标系xOy中,反比例函数图象与直线y=x-2相交于横坐标为3的点A.(1)求反比例函数的解析式;
(2)如果点B在直线y=x-2上,点C在反比例函数图象上,BC∥x轴,BC=4,且BC在点A上方,求点B的坐标.
分析 (1)设反比例函数的解析式为y=$\frac{k}{x}$,把点A的横坐标代入直线解析式y=x-2,可求得点A的纵坐标,把点A的横纵坐标代入y=$\frac{k}{x}$,即可求得所求的反比例函数解析式;
(2)设点C($\frac{3}{m}$,m),则点B(m+2,m),根据BC=4列出方程m+2-$\frac{3}{m}$=4,解方程即可.
解答 解:(1)设反比例函数的解析式为y=$\frac{k}{x}$.
∵横坐标为3的点A在直线y=x-2上,
∴y=3-2=1,
∴点A的坐标为(3,1),
∴1=$\frac{k}{3}$,∴k=3,
∴反比例函数的解析式为y=$\frac{3}{x}$;
(2)设点C($\frac{3}{m}$,m),则点B(m+2,m),
∵BC=4,
∴m+2-$\frac{3}{m}$=4,
∴m2+2m-3=4m,
∴m2-2m-3=0,
解得m1=3,m2=-1.
m1=3,m2=-1都是方程的解,但m=-1不符合题意,
∴点B的坐标为(5,3).
点评 本题考查了反比例函数与一次函数的交点问题,待定系数法求反比例函数的解析式,一次函数、反比例函数图象上点的坐标特征,难度适中.求出反比例函数的解析式是解题的关键.

练习册系列答案
相关题目
11.数据6,7,7,6,13,5,6,8的众数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 5或6或7 |
8.如果关于x的方程x2-x+m=0有实数根,那么m的取值范围是( )
| A. | m>$\frac{1}{4}$ | B. | m≥$\frac{1}{4}$ | C. | m<$\frac{1}{4}$ | D. | m≤$\frac{1}{4}$ |
5.下列事件中,是确定事件的是( )
| A. | 上海明天会下雨 | B. | 将要过马路时恰好遇到红灯 | ||
| C. | 有人把石头孵成了小鸭 | D. | 冬天,盆里的水结成了冰 |
9.边长为a的正六边形的面积为( )
| A. | $\frac{3\sqrt{3}}{2}$a2 | B. | 6a2 | C. | $\frac{\sqrt{3}}{4}$a2 | D. | 3$\sqrt{3}$a2 |
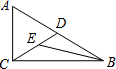 如图,在Rt△ABC中,∠ACB=90°,AB=2AC,点E在中线CD上,BE平分∠ABC,那么∠DEB的度数是45°.
如图,在Rt△ABC中,∠ACB=90°,AB=2AC,点E在中线CD上,BE平分∠ABC,那么∠DEB的度数是45°. 如图,等腰△ABC内接于半径为5的⊙O,AB=AC,tan∠ABC=$\frac{1}{3}$.求BC的长.
如图,等腰△ABC内接于半径为5的⊙O,AB=AC,tan∠ABC=$\frac{1}{3}$.求BC的长.