题目内容
15.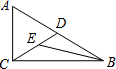 如图,在Rt△ABC中,∠ACB=90°,AB=2AC,点E在中线CD上,BE平分∠ABC,那么∠DEB的度数是45°.
如图,在Rt△ABC中,∠ACB=90°,AB=2AC,点E在中线CD上,BE平分∠ABC,那么∠DEB的度数是45°.
分析 先由∠ACB=90°,AB=2AC,根据三角函数求出∠ABC的度数为30°,然后根据直角三角形斜边上的中线等于斜边的一半得到CD=BD,然后根据等边对等角可得∠ABC=∠DCB=30°,进而根据三角形内角和定理可得:∠BDC=120°,然后根据角平分线的定义可得∠DBE=$\frac{1}{2}$∠ABC=15°,最后根据三角形内角和定理可得:∠DEB的度数.
解答 解:在Rt△ABC中,∵∠ACB=90°,AB=2AC,
∴sin∠ABC=$\frac{AC}{AB}=\frac{1}{2}$,
∴∠ABC=30°,
∵CD是AB边上的中线,
∴CD=BD=AD=$\frac{1}{2}$AB,
∴∠ABC=∠DCB=30°,
∵∠ABC+∠DCB+∠CDB=180°,
∴∠CDB=120°,
∵BE平分∠ABC,
∴∠DBE=$\frac{1}{2}$∠ABC=15°,
∵∠CDB+∠DBE+∠DEB=180°,
∴∠DEB=45°.
故答案为:45°.
点评 此题考查了含30度角的直角三角形,及角平分线的定义,直角三角形斜边中线的性质,三角形内角和定理,解题的关键是:根据三角函数值求出∠ABC的度数为30°.

练习册系列答案
相关题目
3.已知一水池的容积V(公升)与注入水的时间t(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
(1)求这段时间时V关于t的函数关系式(不需要写出函数的定义域);
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
| 注入水的时间t(分钟) | 0 | 10 | … | 25 |
| 水池的容积V(公升) | 100 | 300 | … | 600 |
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
10.下列图形中,是轴对称图形,但不是中心对称图形的是( )
| A. | 正三角形 | B. | 正六边形 | C. | 平行四边形 | D. | 菱形 |
5.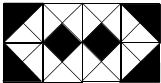 甲、乙两人打赌,各自往图中的区域掷石子,若落在阴影部分上甲获胜,若落在白色部分上乙获胜,则甲、乙获胜的概率情况是( )
甲、乙两人打赌,各自往图中的区域掷石子,若落在阴影部分上甲获胜,若落在白色部分上乙获胜,则甲、乙获胜的概率情况是( )
 甲、乙两人打赌,各自往图中的区域掷石子,若落在阴影部分上甲获胜,若落在白色部分上乙获胜,则甲、乙获胜的概率情况是( )
甲、乙两人打赌,各自往图中的区域掷石子,若落在阴影部分上甲获胜,若落在白色部分上乙获胜,则甲、乙获胜的概率情况是( )| A. | 甲大 | B. | 乙大 | C. | 相等 | D. | 不确定 |
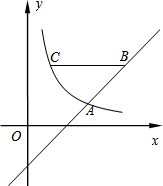 如图,在直角坐标系xOy中,反比例函数图象与直线y=x-2相交于横坐标为3的点A.
如图,在直角坐标系xOy中,反比例函数图象与直线y=x-2相交于横坐标为3的点A. 如图,在四边形ABCD中,AD∥BC,AB=AC,BE=CE=AD.
如图,在四边形ABCD中,AD∥BC,AB=AC,BE=CE=AD.