题目内容
10.(1)已知:如图1,在矩形ABCD中,点E,F分别在AB,CD边上,BE=DF,连接CE,AF.求证:AF=CE.(2)如图2,AB切⊙O于点B,OA=2,∠OAB=30°,弦BC∥OA.求:劣弧BC的长.(结果保留π)
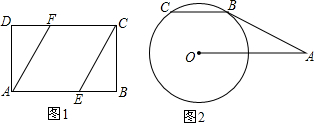
分析 (1)由矩形的性质得DC∥AB,DC=AB,由于DF=BE,则CF=AE,于是可判断四边形AFCE是平行四边形,然后根据平行四边形的性质得AF=CE;
(2)连接OC,OB,如图,根据切线的性质得∠ABO=90°,在Rt△ABO中利用含30度的直角三角形三边的关系得到OB=$\frac{1}{2}$OA=1,且∠AOB=60°,再利用BC∥OA得到∠OBC=∠AOB=60°,则可判断△BOC为等边三角形,所以∠BOC=60°,然后利用弧长公式计算劣弧BC的长.
解答 (1)证明:如图: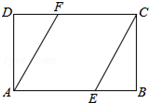
∵四边形ABCD是矩形,
∴DC∥AB,DC=AB,
∴CF∥AE,
∵DF=BE,
∴CF=AE,
∴四边形AFCE是平行四边形,
∴AF=CE;
(2)解:连接OC,OB,如图,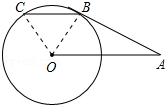
∵AB为圆O的切线,
∴∠ABO=90°,
在Rt△ABO中,∵OA=2,∠OAB=30°,
∴OB=$\frac{1}{2}$OA=1,∠AOB=60°,
∵BC∥OA,
∴∠OBC=∠AOB=60°,
而OB=OC,
∴△BOC为等边三角形,
∴∠BOC=60°,
∴劣弧BC的长=$\frac{60•π•1}{180}$=$\frac{1}{3}$π.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点;经过切点且垂直于切线的直线必经过圆心.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了矩形的性质、平行四边形的判定与性质和弧长公式.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
15.已知点A(-3,a),B(-1,b),C(3,c)都在反比例函数y=$\frac{4}{x}$的图象上,则a,b,c大小关系是( )
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | c>a>b |
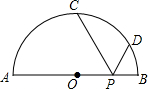 如图,AB是半径为R的半圆的直径,C、D是半圆周上的两点,已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°,动点P在线段AB上,则PC+PD的最小值是$\sqrt{3}$R.
如图,AB是半径为R的半圆的直径,C、D是半圆周上的两点,已知$\widehat{AC}$、$\widehat{BD}$的度数分别是90°和30°,动点P在线段AB上,则PC+PD的最小值是$\sqrt{3}$R.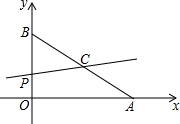 如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点
如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点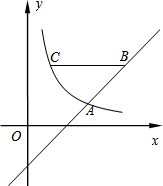 如图,在直角坐标系xOy中,反比例函数图象与直线y=x-2相交于横坐标为3的点A.
如图,在直角坐标系xOy中,反比例函数图象与直线y=x-2相交于横坐标为3的点A.