题目内容
8.如果关于x的方程x2-x+m=0有实数根,那么m的取值范围是( )| A. | m>$\frac{1}{4}$ | B. | m≥$\frac{1}{4}$ | C. | m<$\frac{1}{4}$ | D. | m≤$\frac{1}{4}$ |
分析 根据方程x2-x+m=0有实数根得到△=(-1)2-4m≥0,求出m的取值范围即可.
解答 解:∵关于x的方程x2-x+m=0有实数根,
∴△≥0,
∴(-1)2-4m≥0,
∴m≤$\frac{1}{4}$,
故选:D.
点评 本题考查了根的判别式,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
3.已知一水池的容积V(公升)与注入水的时间t(分钟)之间开始是一次函数关系,表中记录的是这段时间注入水的时间与水池容积部分对应值.
(1)求这段时间时V关于t的函数关系式(不需要写出函数的定义域);
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
| 注入水的时间t(分钟) | 0 | 10 | … | 25 |
| 水池的容积V(公升) | 100 | 300 | … | 600 |
(2)从t为25分钟开始,每分钟注入的水量发生变化了,到t为27分钟时,水池的容积为726公升,如果这两分钟中的每分钟注入的水量增长的百分率相同,求这个百分率.
13.某工厂对一个小组生产的零件进行调查.在10天中,这个小组出次品的情况如表所示:
那么在这10天中这个小组每天所出次品数的标准差是$\sqrt{2}$.
| 每天出次品的个数 | 0 | 2 | 3 | 4 |
| 天数 | 3 | 2 | 4 | 1 |
18. 某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
 某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )
某校九(3)班的全体同学喜欢的球类运动用如图所示的统计图来表示,下面说法正确的是( )| A. | 从图中可以直接看出喜欢各种球类的具体人数 | |
| B. | 从图中可以直接看出全班的总人数 | |
| C. | 从图中可以直接看出全班同学初中三年来喜欢各种球类的变化情况 | |
| D. | 从图中可以直接看出全班同学现在喜欢各种球类人数的大小关系 |
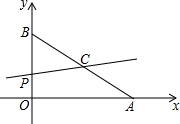 如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点
如图,平面直角坐标系中,已知点A(4,0)和点B(0,3),点C是AB的中点,点P在折线AOB上,直线CP截△AOB,所得的三角形与△AOB相似,那么点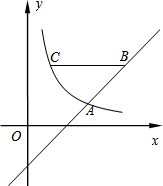 如图,在直角坐标系xOy中,反比例函数图象与直线y=x-2相交于横坐标为3的点A.
如图,在直角坐标系xOy中,反比例函数图象与直线y=x-2相交于横坐标为3的点A. 如图,△ABC中,AB=AC,点D,E在BC边上,当BD=CE时,△ABD≌△ACE.(添加一个适当的条件即可)
如图,△ABC中,AB=AC,点D,E在BC边上,当BD=CE时,△ABD≌△ACE.(添加一个适当的条件即可)